A cubeword is a special type of a crossword. When building a cubeword, you start by choosing a positive integer $a$: the side length of the cube. Then, you build a big cube consisting of $a×a×a$ unit cubes. This big cube has $12$ edges. Then, you discard all unit cubes that do not touch the edges of the big cube. The figure below shows the object you will get for $a = 6$.
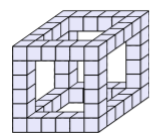
Finally, you assign a letter to each of the unit cubes in the object. You must get a meaningful word along each edge of the big cube. Each edge can be read in either direction, and it is sufficient if one of the two directions of reading gives a meaningful word.
The figure below shows the object for $a = 6$ in which some unit cubes already have assigned letters. You can already read the words ‘SUBMIT’, ‘ACCEPT’ and ‘TURING’ along three edges of the big cube.
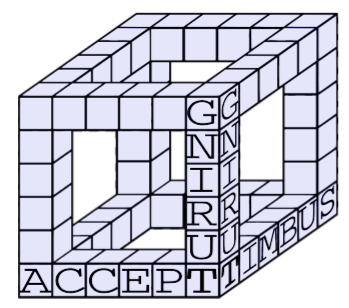
You are given a list of valid words. Each word from the wordlist may appear on arbitrarily many edges of a valid cubeword. Find and report the number of different cubewords that can be constructed, modulo $998,244,353$.
If one cubeword can be obtained from another by rotation or mirroring, they are considered distinct.
The first line contains a single integer $n (1 ≤ n ≤ 100,000)$ – the number of words.
Then, $n$ lines follow. Each of these lines contains one word that can appear on the edges of the big cube. The length of each word is between $3$ and $10$, inclusive.
It is guaranteed that all words are different.
Output a single integer, the number of distinct cubewords for the given list of valid words modulo $998,244,353$.
Comet OJ1
radar11
robot22
FLOW
WOLF22
baobab
bob40973
TURING
SUBMIT
ACCEPT1623
MAN1LA
MAN6OS
AN4NAS114Subtask 1 (21 points): the words consist only of letters ‘a’ - ‘f’ (lowercase)
Subtask 2 (29 points): the words consist only of letters ‘a’ - ‘p’ (lowercase)
Subtask 3 (34 points): the words consist of letters ‘a’ - ‘p’ (lowercase) and ‘A’ - ‘P’ (uppercase)
Subtask 4 (16 points): the words consist of letters ‘a’ - ‘z’ (lowercase), ‘A’ - ‘Z’ (uppercase) and digits ‘0’ - ‘9’