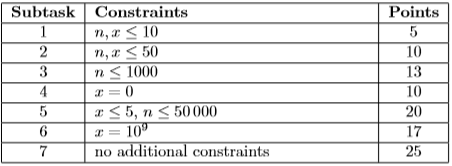
Global warming is an important issue and Johnny knows about it. He decided to make an analysis of historical temperatures and find a subsequence of days (not necessarily consecutive) where the temperature was strictly increasing. It will convince the non-believers!
Johnny has found historical data from $n$ consecutive days. The temperature on the $i$-th day was $t_i$.
Formally, we are interested in finding the length of the longest increasing subsequence (LIS) of $(t_1,t_2,...,t_n)$, that is, the largest possible $k$ for which it is possible to choose an increasing sequence of indices $1 ≤ a_1 < a_2 < ... < a_k ≤ n$ such that $t_{a_1} < t_{a_2} < ... < t_{a_k}$.
Johnny wants to find a really long subsequence and that is why he decided to cheat a bit. He will first choose a non-empty interval of days and an integer $d (−x ≤ d ≤ x)$ and he will increase the temperature in each of those days by $d$. A small change like that probably will not be noticed by the community, while at the same time it should make the LIS longer. It is allowed to choose $d = 0$.
What is the largest possible length of the LIS after a change?