《血源》因为玩家很容易死亡而常被称作一款充满制作人恶意的游戏。一款游戏在开发过程中通常会进行许多修改，《血源》自然也不例外，但是制作人时常会担心修改之后的游戏不够恶意。他希望在每次对游戏进行修改之后，计算玩家有多少种可能的死亡路线。因为游戏的开发进度不能太慢，所以计算的过程需要尽可能的快。
为了简化问题，我们可以把《血源》的地图看作$n$个大区域，从第$i$个大区域可以直接走到第$i+1$个大区域。每个大区域内有$3$个小区域。我们用$p_i[j][k](1 \le i < n,1 \le j,k \le 3)$表示玩家从第$i$个大区域的第$j$个小区域走到第$i+1$个大区域的第$k$个小区域时的不同的死亡方式的数量。我们假设玩家行进时不会在同一个大区域的不同小区域之间移动。
你需要支持以下两种操作：
$1 \; l \; r \; p$：将$p_l,p_{l+1},\cdots,p_r$全部修改为$p$。
$2 \; l \; r$：查询若玩家从第$l$个大区域出发走到第$r$个大区域，一共有多少种不同的死亡路线。在这里，我们假设从第$l,l+1,\cdots,r-1$个大区域移动到下一个大区域时会恰好死亡一次。两个死亡路线不同当且仅当两个路线中，玩家经过的小区域不完全相同或某次移动时的死亡方式不同。
请参考样例解释来获得更详细的死亡路线的计算方式。
第一行有两个整数$n,m(2 \le n,m \le 10^5)$分别代表地图中大区域的数量与操作数量。
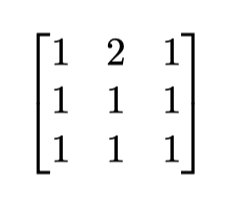
接下来有$3(n-1)$行，每行$3$个整数。$p_i[j][k](1 \le i <n, 1\le j,k \le 3, 1 \le p_i[j][k] \le 10^8)$由其中的第$3(i-1)+j$行的第$k$个整数表示。
接下来有$m$个操作需要描述。每个操作的第一行第一个整数$op(1 \le op \le 2)$代表操作类型。
如果操作类型为$1$，接下来两个整数$l,r(1 \le l \le r < n)$表示修改的范围。接下来$3$行每行包含$3$个整数，第$i$行的第$j$个整数代表$p[i]j$。
如果操作类型为$2$，接下来两个整数$l,r(1 \le l < r \le n)$表示查询的范围。
对于每个类型为$2$的操作，输出玩家的不同死亡路线的个数模$998244353$的值。
Comet OJ3 4
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
2 1 2
2 1 3
1 1 1
1 2 1
1 1 1
1 1 1
2 1 3
9
27
30
初始时从任何大区域的任何小区域前往下一个大区域的任何小区域的路上的死亡方式都恰好有$1$种。
第一个操作查询从大区域$1$到大区域$2$的死亡路线数量。以经过的区域划分，有
大区域$1$中的小区域$1$ $\rightarrow$ 大区域$2$中的小区域$1$
大区域$1$中的小区域$1$ $\rightarrow$ 大区域$2$中的小区域$2$
大区域$1$中的小区域$1$ $\rightarrow$ 大区域$2$中的小区域$2$
大区域$1$中的小区域$1$ $\rightarrow$ 大区域$2$中的小区域$3$
大区域$1$中的小区域$2$ $\rightarrow$ 大区域$2$中的小区域$1$
$\cdots$
大区域$1$中的小区域$3$ $\rightarrow$ 大区域$2$中的小区域$3$ 共$9$种可能，每种可能中仅有$1$种死亡方式的组合，故有$9$种死亡路线。
第二个操作查询从大区域$1$到大区域$3$的死亡路线数量。以经过的区域划分，有
大区域$1$中的小区域$1$ $\rightarrow$ 大区域$2$中的小区域$1$ $\rightarrow$ 大区域$3$中的小区域$1$
大区域$1$中的小区域$1$ $\rightarrow$ 大区域$2$中的小区域$1$ $\rightarrow$ 大区域$3$中的小区域$2$
大区域$1$中的小区域$1$ $\rightarrow$ 大区域$2$中的小区域$1$ $\rightarrow$ 大区域$3$中的小区域$3$
大区域$1$中的小区域$1$ $\rightarrow$ 大区域$2$中的小区域$2$ $\rightarrow$ 大区域$3$中的小区域$1$
$\cdots$
大区域$1$中的小区域$2$ $\rightarrow$ 大区域$2$中的小区域$1$ $\rightarrow$ 大区域$3$中的小区域$1$
$\cdots$
大区域$1$中的小区域$3$ $\rightarrow$ 大区域$2$中的小区域$3$ $\rightarrow$ 大区域$3$中的小区域$3$
共$27$种可能，每种可能中仅有$1$种死亡方式的组合，故有$27$种死亡路线。
第三个操作将大区域$1$前往下一个区域（即大区域$2$）的死亡方式个数改为
第四个操作查询从大区域$1$到大区域$3$的死亡路线数量。以经过的区域划分，和第二个操作的划分方式相同，其中 大区域$1$中的小区域$1$ $\rightarrow$ 大区域$2$中的小区域$2$ $\rightarrow$ 大区域$3$ 的$3$种可能，对应$2$种死亡方式的组合，其它可能都对应$1$种死亡方式，故有$30$种死亡路线。