Comet OJ

C1647 [Wannafly冬令营2018Day2]Honeycomb

内存限制：256 MB 时间限制：4000 ms

题目描述

蜂窝是由一系列六边形棱柱格子组成，其中每个格子有六个相邻的格子，而每两个相邻的格子共享一条边界。 这里有些边界是可穿行的，但有些则不是。

小汉是一个勤劳的工蜂，他每天都在为打通边界或是切断两个相邻格子的联系辛苦工作着。几天后，他将有机会任意改动一片蜂窝的格局。这片蜂窝与外界不连通，包含如下图所示的 $n$ 行 $m$ 列格子。

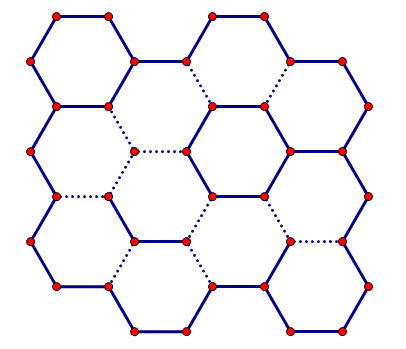
honeycomb.png

为了切断两个格子的联系，他可能需要将某些边界设为不可穿行。他很好奇这至少要改动多少条边才能实现，你能帮他计算出，对于任意两个特别的格子，他最少需要改动的边数吗？为了避免输出过大，你只需要给出这些最小边数的之和即可。

输入格式

输入包含多组测试数据。第一行包含一个整数 $T$，表示测试数据的组数。随后的内容是各组测试数据。对于每组测试数据：

第一行包含两个整数 $n$ 和 $m$。

接下来 $(4 n + 3)$ 行描述了这片蜂窝，其中每一行至多有 $(6 m + 3)$ 个字符。奇数行包含用加号（+）表示的顶点和水平方向的边界，而偶数行包含对角线方向的边界。

具体来说，每个格子由 $6$ 个顶点和 $6$ 条边界组成，每条边所示的字符会恰好位于对应端点之间，其中可穿行的边用空格（）表示，不可穿行的边遵循如下规则：

  • 每个格子的上边界或下边界由三个连续的减号（-）或三个连续的空格表示，取决于它是否可以被穿行；
  • 每个格子的每条不可穿行的对角线边界由一个正斜线（/）或一个反斜线（\）字符表示，取决于它的方向。

此外，在每个特别的格子中心处有一个星号（*）字符。其他字符将会是空白符，且输入每一行不会包含行末空格。

  • $1 \leq T \leq 100$
  • $2 \leq n, m \leq 100$
  • 所有测试数据的特别格子的数量之和不超过 $3000$。
  • 保证每个不特别的格子没有可以穿行的边界。

输出

对于每组测试数据，输出一行Case #x: y，其中x是测试数据的编号（从 $1$ 开始编号），y是这组数据的答案。

样例

样例输入 1

2
2 2
  +---+
 /     \
+   *   +---+
 \     /     \
  +---+   *   +
 /           /
+   *   +   +
 \           \
  +---+   *   +
       \     /
        +---+
2 3
  +---+       +---+
 /     \     /     \
+   *   +---+       +
 \           \     /
  +---+   *   +---+
 /                 \
+   *   +---+   *   +
 \                 /
  +---+   *   +---+
       \     /
        +---+

样例输出 1

Case #1: 6
Case #2: 16

提示