【样例说明】
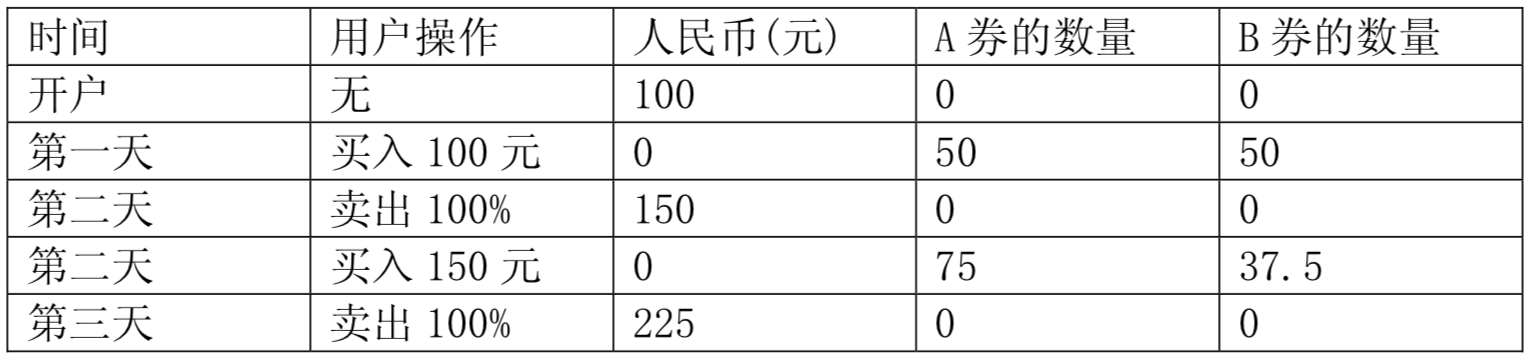
【评分方法】
本题没有部分分,你的程序的输出只有和标准答案相差不超过0.001时,才能获得该测试点的满分,否则不得分。
【数据规模和约定】
测试数据设计使得精度误差不会超过 $10^{-7}$。
对于 $40\%$ 的测试数据,满足 $N ≤ 10$;
对于 $60\%$ 的测试数据,满足 $N ≤ 1 000$;
对于 $100\%$ 的测试数据,满足 $N ≤ 100 000$;
对于 $100\%$ 的测试数据,满足:$0 < A_K≤ 10$;$0 < B_K≤ 10$;$0 < Rate_K≤ 100$;$MaxProfit ≤ 10^9$。
【提示】
输入文件可能很大,请采用快速的读入方式。
必然存在一种最优的买卖方案满足:
- 每次买进操作使用完所有的人民币;
- 每次卖出操作卖出所有的金券。