Comet OJ

C1466 [AHOI2005]航线规划

内存限制：256 MB 时间限制：1000 ms

题目描述

对 Samuel 星球的探险已经取得了非常巨大的成就，于是科学家们将目光投向了 Samuel 星球所在的星系——一个巨大的由千百万星球构成的 Samuel 星系。星际空间站的 Samuel II 巨型计算机经过长期探测，已经锁定了 Samuel 星系中许多星球的空间坐标，并对这些星球从 $1$ 开始编号 $1$、$2$、$3$……。 一些先遣飞船已经出发，在星球之间开辟探险航线。 探险航线是双向的，例如从 $1$ 号星球到 $3$ 号星球开辟探险航线，那么从 $3$ 号星球到 $1$ 号星球也可以使用这条航线。

例如下图所示：

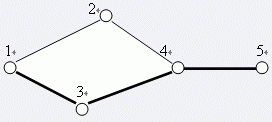
image.png

在 $5$ 个星球之间，有 $5$ 条探险航线。 A、B 两星球之间，如果某条航线不存在，就无法从 A 星球抵达 B 星球，我们则称这条航线为关键航线。 显然上图中，$1$ 号与 $5$ 号星球之间的关键航线有 $1$ 条：即为 $4-5$ 航线。 然而，在宇宙中一些未知的磁暴和行星的冲撞，使得已有的某些航线被破坏，随着越来越多的航线被破坏，探险飞船又不能及时回复这些航线，可见两个星球之间的关键航线会越来越多。 假设在上图中，航线 $4-2$（从 $4$ 号星球到 $2$ 号星球）被破坏。此时，$1$ 号与 $5$ 号星球之间的关键航线就有 $3$ 条：$1-3$，$3-4$，$4-5$。

小联的任务是，不断关注航线被破坏的情况，并随时给出两个星球之间的关键航线数目。现在请你帮助完成。

输入格式

第一行有两个整数 $N$，$M$。表示有 $N$ 个星球（$1< N < 30000$），初始时已经有 $M$ 条航线（$1 < M < 100000$）。随后有 $M$ 行，每行有两个不相同的整数 $A$、$B$ 表示在星球 A 与 B 之间存在一条航线。

接下来每行有三个整数 $C$、$A$、$B$。$C$ 为 $1$ 表示询问当前星球 A 和星球 B 之间有多少条关键航线；C 为 $0$ 表示在星球 A 和星球 B 之间的航线被破坏，当后面再遇到 $C$ 为 $1$ 的情况时，表示询问航线被破坏后，关键路径的情况，且航线破坏后不可恢复； $C$ 为 $-1$ 表示输入结束，这时该行没有 $A,B$ 的值。被破坏的航线数目与询问的次数总和不超过 $40000$。

输出

对每个 $C$ 为 $1$ 的询问，输出一行一个整数表示关键航线数目。

注意：我们保证无论航线如何被破坏，任意时刻任意两个星球都能够相互到达。在整个数据中，任意两个星球之间最多只可能存在一条直接的航线。

样例

样例输入 1

5 5
1 2
1 3
3 4
4 5
4 2
1 1 5
0 4 2
1 5 1
-1

样例输出 1

1
3

提示