Comet OJ
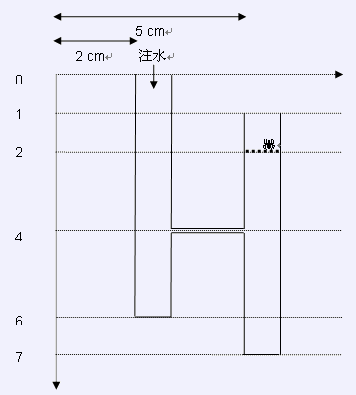
所有位置都用有序数对 $(x, y)$ 表示，其中 $y$ 坐标从上到下逐渐增大；$x$ 坐标从左到右逐渐增大，因此左上角的坐标为 $(0,0)$，其他所有坐标值为 $0$ 到 $100$ 之间的整数。输入第一行为一个整数 $p(1 \le p \le 20)$，表示管道的数目；以下 $p$ 行，每行用 $x, y, h$ 三个整数描述一根管道。$(x,y)$ 为管道左上角坐标；$h$ 为管道高度 $(1 \le h \le 20)$。以下一行为一个整数 $L(0 \le L \le 50)$，为连接的个数。以下 $L$ 行每行用三个整数 $x, y, d$ 描述一个连接，$(x,y)$ 为左端点的坐标，$d$ 为连接的长度 $(1 \le d \le 20)$。最后一行为两个整数 $a, b$，表示 Willy 在管道 $a$ 的 $y$ 坐标为 $b$ 的位置。管道按照在文件中出现的顺序编号为 $1,2,3…p$
以下为一些假设：
- 水源总是在第一根管道的正上方
- 连接不会穿越管道
- 任意两个连接的 $y$ 坐标都不相同
- 任意两个管道的左上角的 $x$ 坐标都不相同
- 任意连接的两个端点都在管道上（不会出现悬空的情形）