[SHOI2008]安全的航线

内存限制：256 MB 时间限制：1000 ms

在设计航线的时候，安全是一个很重要的问题。首先，最重要的是应采取一切措施确保飞行不会发生任何事故，但同时也需要做好最坏的打算，一旦事故发生，就要确保乘客有尽量高的生还几率。当飞机迫降到海上的时候，最近的陆地就是一个关键的因素。航线中最危险的地方就是距离最近的陆地最远的地方，我们称这种点为这条航线“孤地点”。孤地点到最近陆地的距离被称为“孤地距离”。作为航空公司的高级顾问，你接受的第一个任务就是尽量找出一条航线的孤地点，并计算这条航线的孤地距离。为了简化问题，我们认为地图是一个二维平面，陆地可以用多边形近似，飞行线路为一条折线。航线的起点和终点都在陆地上，但中间的转折点是可能在海上（如下图所示，方格标示出了孤地点）。

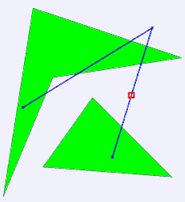
输入的第一行包括两个整数 $C$ 和 $N$（$1≤C≤20$，$2≤N≤20$），分别代表陆地的数目的航线的转折点的数目。接下来有 $N$ 行，每行有两个整数 $x,y$。$(x,y)$ 表示一个航线转折点的坐标，第一个转折点为航线的起点，最后一个转折点为航线的终点。接下来的输入将用来描述 $C$ 块大陆。每块输入由一个正整数 $M$ 开始（$M≤30$），$M$ 表示多边形的顶点个数，接下来的 $M$ 行，每行会包含两个整数 $x,y$，$(x,y)$ 表示多边形的一个顶点坐标，我们保证这些顶点以顺时针或逆时针给出了该多边形的闭包，不会出现某些边相交的情况。此外我们也保证输入数据中任何两块大陆不会相交。输入的所有坐标将保证在 $-10000$ 到 $10000$ 的范围之间。

输出一个浮点数，表示航线的孤地距离，数据保留 $2$ 位小数。

样例输入 1

样例输出 1

0.00