[JSOI2013]投影面积

内存限制：256 MB 时间限制：1000 ms

为了简单起见，投影屏幕对应二维平面中的一条平行于 $x$ 轴，连接点 $(x_1^S,y^S)$ 和点 $(x_2^S,y^S)$ 的线段。

JYY 的投影仪位于原点，朝向 $y$ 轴正方向，发出对称于 $y$ 轴并且张角度数为 $ang$ 的光束。如下图所示（粗线条为投影屏幕，黄色区域为投影仪射出的光束）。

实验室内一共有 $N$ 个障碍物，每个障碍物都对应于二维平面中的一条线段（我们认为这些障碍物的厚度为 $0$）。

有一些障碍物是不能反光的，因此光线只要射到这些线段上，就会被完全吸收（比如投影屏幕就是不会反光的）；其他的障碍物则是双面可以反光的，光线如果射到这些线段上，就会按照基本广学院里进行反射。

所有的障碍物都相互不接触，并且也不会与投影屏幕，或者坐标原点接触。

光线在空气中传播会有损耗。因此在JYY的实验室中，光线在传播了 $len$ 的距离之后，就会消失。

现在 JYY 想知道，投影屏幕上被照亮的区域，占投影屏幕总长度的比率。

第一行包含一个整数与两个正实数，分别为 $N,ang,len$。

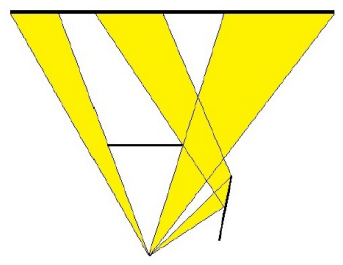
接下来 $N$ 行，每行 $5$ 个整数，$x_1,y_1,x_2,y_2,r$，表示 JYY 的实验室里存在一个连接点 $(x_1,y_1)$ 和点 $(x_2,y_2)$ 的障碍物。$r$ 为 $0$ 或者 $1$。当 $r=0$ 时，表示这个障碍物不反光；当 $r=1$ 时，表示这个障碍物是完全双面反光的。

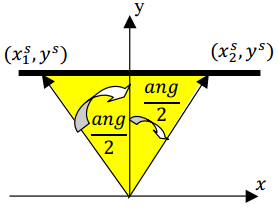
接下来一行，包含四个整数，$x_1^S,y^S,x_2^S,y^S$，表示投影屏幕的位置。这一行的第二个和第四个整数一定是相同的。

输入数据保证 $y^S>0,x_1^S<x_2^S$，并且对于任意障碍物，满足 $|y_2|<y^S$。

输入数据还保证，对于一条光线，在其消失或者被吸收之前，至多反射 $30$ 次。

输出一行包含一个 $0$ 到 $1$ 之间的实数，表示屏幕上被照亮部分的长度与屏幕总长的比值。

结果精确到小数点后 $4$ 位。

样例输入 1

2 150.0000 1000.0000
-60 165 50 165 0
110 25 130 120 1
-205 360 275 360

样例输出 1

0.7443

$0 \le N \le 10, 0 < ang \le 150, 0 < len \le 1000$，并且任意输入坐标的绝对值不超过 $1000$。

样例图解如下

C1277 [JSOI2013]投影面积

题目描述

输入格式

输出

样例

样例输入 1

样例输出 1

提示