小渊是个聪明的孩子，他经常会给周围的小朋友们讲些自己认为有趣的内容。最近，他准备给小朋友们讲解彩色水平光源照射下的立体图，并请你帮他在平面上画出来。小渊有一块面积为 $m \times n$ 的矩形区域，上面有 $m \times n$ 个边长为 $1$ 的格子，每个格子上堆了一些同样大小的积木（积木的长宽高都是 $1$）。为了方便阐述，我们假设这块区域是坐北朝南的，下面我们给出一个例子。
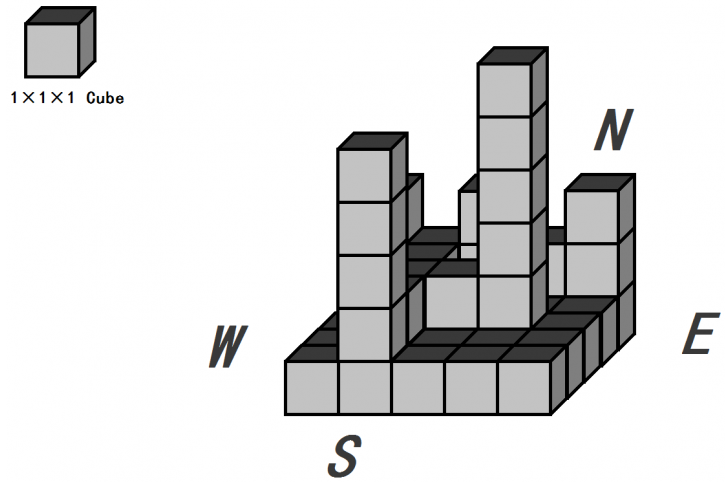
小渊想请你打印出这些格子的立体图。我们定义每个积木为如下格式，并且不会做任何翻转旋转，只会严格以这一种形式摆放（左侧是应该打印出来的图样，右侧为对应每一个位置符号的十进制ASCII，其中ASCII为 32 的符号为空格。
在良好的光学环境下，小渊将 $T$ 束平行光同时照射在这些积木上。这些平行光首先满足一定是红绿蓝三基色之一，其次入射角度满足：与 $x$ 轴 $y$ 轴的夹角度数均为 $45$ 的倍数；且与 $z$ 轴正方向的夹角或为 $45$ 度，或为 $0$ 度，或为 $315$ 度。
具体来说，我们最多会考虑 $9$ 个方向的不同平行光，它们的入射方向可以被描述为：
西北方 $45$ 度仰角 正北方 $45$ 度仰角 东北方 $45$ 度仰角
正西方 $45$ 度仰角 垂直从上入射光 正东方 $45$ 度仰角
西南方 $45$ 度仰角 正南方 $45$ 度仰角 东南方 $45$ 度仰角
对于每一个单位积木来说，可以打印出来的三个表面被分为 $12$ 个小三角形。
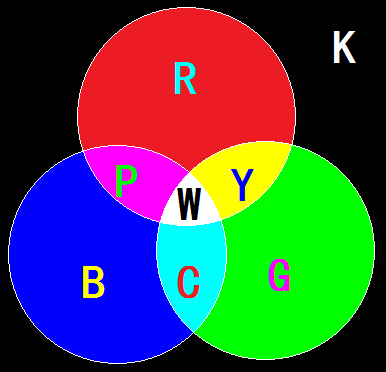
红绿蓝三基色分别用字母RGB来表示。
而二次叠加后的三种颜色青黄紫，分别用YCP来表示。
对于三次叠加后的颜色，也就是白色，用W来表示。
第一行有两个正整数 $m$ 和 $n$，表示区域有 $m$ 行 $n$ 列。之后 $m$ 行，依次由远及近描述了每一行的情况。每一行给出 $n$ 个正整数，表示第 $i$ 行第 $j$ 列中有堆放了多少积木。之后 $3$ 行，每行三个字符，描述了 $9$ 个对应方向（与地图描述方向相同）的光照颜色。其中每一个字符或者为RGB中之一，表示对应的颜色。或者为 $*$，表示没有照射光。这九个方向依次是：
西北方 $45$ 度仰角 正北方 $45$ 度仰角 东北方 $45$ 度仰角
正西方 $45$ 度仰角 垂直从上入射光 正东方 $45$ 度仰角
西南方 $45$ 度仰角 正南方 $45$ 度仰角 东南方 $45$ 度仰角
输出给出了打印后的效果。其中要求输出结果不含前导空行，结尾也没有额外空行。输出的第一列不能全是空格，且每一行末尾也没有额外空格。
Comet OJ2 2
2 1
1 1
R**
***
**G+-------+
/Y\YYYY’/|
/YY.*’YY/G|
/.YYYY\Y/G/|
+-------+G.G|
|\GGGGG/|\:G|
|G\GGG/G|G*G|
|GG\G/GG|G:\|
|GGGXGGG|G’G+-------+
|GG/G\GG|/G/G\YYYY’/|
|G/GGG\G|G/GG.*’YY/G|
|/GGGGG\|/.GGGG\Y/G/|
+-------+-------+G.G|
/Y\GGGG’/G\GGGG’/|\:G|
/YY.*’GG/GG.*’GG/G|G*G|
/.YYYY\G/.GGGG\G/G/|G:\|
+-------+-------+G.G|G’G+
|\GGGGG/|\GGGGG/|\:G|/G/
|G\GGG/G|G\GGG/G|G*G|G/
|GG\G/GG|GG\G/GG|G:\|/
|GGGXGGG|GGGXGGG|G’G+
|GG/G\GG|GG/G\GG|/G/
|G/GGG\G|G/GGG\G|G/
|/GGGGG\|/GGGGG\|/
+-------+-------+3 4
1 1 2 1
1 2 1 2
2 1 2 1
**B
***
R*G+-------+
/W\WWWW’/|
/WW.*’WW/C|
/.WWWW\W/C/|
+-------+-------+-------+
/W\WWWW’/|\YYYYY/W\WWWW’/|
/WW.*’WW/C|G\YYY/WW.*’WW/C|
/.WWWW\W/C/|GG\Y/.WWWW\W/C/|
+-------+-------+-------+-------+C.C|---+
/W\WWWW’/|\YYYYY/W\WWWW’/|\YYYYY/|\:C|C’/|
/WW.*’WW/C|G\YYY/WW.*’WW/C|G\YYY/Y|C*C|C/C|
/.WWWW\W/C/|GG\Y/.WWWW\W/C/|GG\Y/YY|C:\|/C/|
+-------+C.G|GGG+-------+C.G|GGGXYYY|C’C+C.C|
|\YYYYY/|\:G|GG/|\YYYYY/|\:G|GG/G\YY|/C/|\:C|
|Y\YYY/Y|C*G|G/K|Y\YYY/Y|C*G|G/GGG\Y|C/C|C*C|
|YY\Y/YY|C:\|/KK|YY\Y/YY|C:\|/GGGGG\|/C/|C:\|
|YYYXYYY|C’G+---|YYYXYYY|C'G+-------+C.C|C’C+
|YY/Y\YY|/G/G\KK|YY/Y\YY|/G/G\GGGG’/|\:C|/C/
|Y/YYY\Y|G/GG.*’|Y/YYY\Y|G/GG.*’WW/C|C*C|C/
|/YYYYY\|/.YYYY\|/YYYYY\|/.WWWW\W/C/|C:\|/
+-------+-------+-------+-------+C.C|C’C+
|\YYYYY/|\YYYYY/|\YYYYY/|\YYYYY/|\:C|/C/
|Y\YYY/Y|Y\YYY/Y|Y\YYY/Y|Y\YYY/Y|C*C|C/
|YY\Y/YY|YY\Y/YY|YY\Y/YY|YY\Y/YY|C:\|/
|YYYXYYY|YYYXYYY|YYYXYYY|YYYXYYY|C’C+
|YY/Y\YY|YY/Y\YY|YY/Y\YY|YY/Y\YY|/C/
|Y/YYY\Y|Y/YYY\Y|Y/YYY\Y|Y/YYY\Y|C/
|/YYYYY\|/YYYYY\|/YYYYY\|/YYYYY\|/对于 $15\%$ 的数据，$1 \le n,m \le 100$，没有入射光。
对于 $40\%$ 的数据，$1 \le n,m \le 100$，入射光只有一束，且入射方向一定是东南方。
对于 $100\%$ 的数据，$1 \le n,m \le 100$，每一个位置堆放的积木总数不超过 $100$，入射光颜色可能是RGB中的任何一种颜色，最多可以有 $9$ 束入射光。