在一个 $n \times m$ 的棋盘上,每个格子有一个权值,初始时,在某个格子的顶点处一只面朝北的蚂蚁,我们只知道它的行走路线是如何转弯,却不知道每次转弯前走了多长。蚂蚁转弯是有一定特点的,即它的转弯序列一定是如下的形式:
右转,右转,左转,左转,右转,右转…左转,左转,右转,右转,右转。
即两次右转和两次左转交替出现的形式,最后两次右转(最后两次一定是右转)后在多加一次右转。我们还知道,蚂蚁不会在同一个位置连续旋转两次,并且蚂蚁行走的路径除了起点以外,不会到达同一个点多次,它最后一定是回到起点然后结束自己的行程,而且蚂蚁只会在棋盘格子的顶点处转弯。
设 $k$ 为蚂蚁左转的次数除以 $2$,当 $k=0$ 时,蚂蚁可能行走的路径如下图:
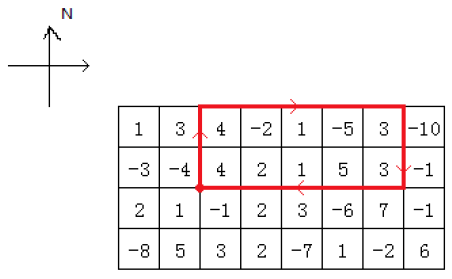
转弯序列为:右转,右转,右转。
当 $k=1$ 时,蚂蚁可能行走的路径如下图:
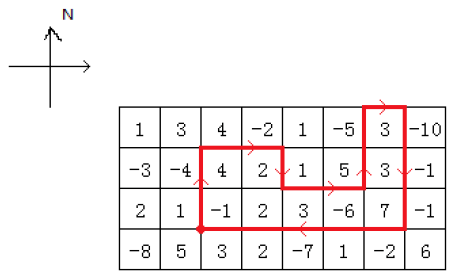
转弯序列为:右转,右转,左转,左转,右转,右转,右转。
现在已知棋盘大小、每个格子的权值以及左转次数 $/2$ 的值,问蚂蚁的路径围出的封闭图形,权值之和最大可能是多少。