C0833 [ZJOI2012]网络

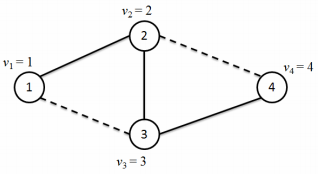
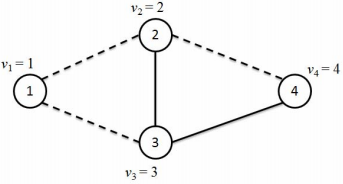
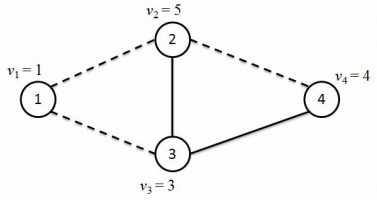
输入的第一行包含四个正整数 $N, M, C, K$，其中 $N$ 为节点个数，$M$ 为边数，$C$ 为边的颜色数，$K$ 为操作数。接下来 $N$ 行，每行一个正整数 $v_i$，为节点 $i$ 的权值。之后 $M$ 行，每行三个正整数 $u, v, w$，为一条连接节点 $u$ 和节点 $v$ 的边，颜色为 $w$。满足 $1 ≤ u, v ≤ N$，$0 ≤ w < C$，保证 $u ≠ v$，且任意两个节点之间最多存在一条边（无论颜色）。最后 $K$ 行，每行表示一个操作。每行的第一个整数 $k$ 表示操作类型。

1. $k = 0$ 为修改节点权值操作，之后两个正整数 $x$ 和 $y$，表示将节点 $x$ 的权值 $v_x$ 修改为 $y$。
2. $k = 1$ 为修改边的颜色操作，之后三个正整数 $u, v$ 和 $w$，表示将连接节点 $u$ 和节点 $v$ 的边的颜色修改为颜色 $w$。满足 $0 ≤ w < C$。
3. $k = 2$ 为查询操作，之后三个正整数 $c, u$ 和 $v$，表示查询所有可能在节点 $u$ 到节点 $v$ 之间的由颜色 $c$ 构成的简单路径上的节点的权值的最大值。如果不存在 $u$ 和 $v$ 之间不存在由颜色 $c$ 构成的路径，那么输出“-1”。
   

输出包含若干行，每行输出一个对应的信息。

1. 对于修改节点权值操作，不需要输出信息。
2. 对于修改边的颜色操作，按以下几类输出：
   1. 若不存在连接节点 $u$ 和节点 $v$ 的边，输出“No such edge.”。
   2. 若修改后不满足条件 $1$，不修改边的颜色，并输出“Error 1.”。
   3. 若修改后不满足条件 $2$，不修改边的颜色，并输出“Error 2.”。
   4. 其他情况，成功修改边的颜色，并输出“Success.”。输出满足条件的第一条信息即可，即若同时满足 $b$ 和 $c$，则只需要输出“Error 1.”。
3. 对于查询操作，直接输出一个整数。

【样例说明】

颜色 $0$ 为实线的边，颜色 $1$ 为虚线的边，由颜色 $0$ 构成的从节点 $1$ 到节点 $4$ 的路径有 $1 – 2 – 4$，故 $\max\{v_1, v_2, v_4\} = \max\{ 1, 2, 4 \} = 4$。将连接节点 $1$ 和节点 $2$ 的边修改为颜色 $1$，修改成功，输出“Success.”

将连接节点 $4$ 和节点 $3$ 的边修改为颜色 $1$，由于修改后会使得存在由颜色 $1$ 构成的环 $( 1 – 2 – 4 – 3 – 1 )$，不满足条件 $2$，故不修改，并输出“Error 2”。不存在颜色 $0$ 构成的从节点 $1$ 到节点 $4$ 的边，输出“-1”。将连接节点 $2$ 和节点 $3$ 的边修改为颜色 $1$，由于修改后节点 $2$ 的连出去的颜色为 $1$ 的边有 $3$ 条，故不满足条件 $1$，故不修改，并输出“Error 1.”。将节点 $2$ 的权值修改为 $5$。

由颜色 $1$ 构成的从节点 $1$ 到节点 $4$ 的路径有 $1 – 2 – 4$，故 $\max\{v_1, v_2, v_4\} = \max\{ 1, 5, 4 \} = 5$。

【数据规模】

对于 30% 的数据：$N ≤ 1000，M ≤ 10000，C ≤ 10，K ≤ 1000$。

另有 20% 的数据：$N ≤ 10000，M ≤ 100000，C = 1，K ≤ 100000$。

对于 100% 的数据：$N ≤ 10000，M ≤ 100000，C ≤ 10，K ≤ 100000$。