Comet OJ

C0800 [AHOI/HNOI2018]道路

内存限制：512 MB 时间限制：1000 ms

题目描述

W 国的交通呈一棵树的形状。W 国一共有 $n − 1$ 个城市和 $n$ 个乡村，其中城市从 $1$ 到 $n − 1$ 编号，乡村从 $1$ 到 $n$ 编号，且 $1$ 号城市是首都。道路都是单向的，本题中我们只考虑从乡村通往首都的道路网络。对于每一个城市，恰有一条公路和一条铁路通向这座城市。对于城市 $i$，通向该城市的道路（公路或铁路）的起点，要么是一个乡村，要么是一个编号比 $i$ 大的城市。没有道路通向任何乡村。除了首都以外，从任何城市或乡村出发只有一条道路；首都没有往外的道路。从任何乡村出发，沿着唯一往外的道路走，总可以到达首都。

W 国的国王小 W 获得了一笔资金，他决定用这笔资金来改善交通。由于资金有限，小 W 只能翻修 $n − 1$ 条道路。小 W 决定对每个城市翻修恰好一条通向它的道路，即从公路和铁路中选择一条并进行翻修。小 W 希望从乡村通向城市可以尽可能地便利，于是根据人口调查的数据，小 W 对每个乡村制定了三个参数，编号为 $i$ 的乡村的三个参数是 $a_i$，$b_i$ 和 $c_i$。假设从编号为 $i$ 的乡村走到首都一共需要经过 $x$ 条未翻修的公路与 $y$ 条未翻修的铁路，那么该乡村的不便利值为

$c_i \cdot (ai + x) \cdot (bi + y)$

在给定的翻修方案下，每个乡村的不便利值相加的和为该翻修方案的不便利值。

翻修 $n − 1$ 条道路有很多方案，其中不便利值最小的方案称为最优翻修方案，小 W 自然希望找到最优翻修方案，请你帮助他求出这个最优翻修方案的不便利值。

输入格式

第一行为正整数 $n$。

接下来 $n − 1$ 行，每行描述一个城市。其中第 $i$ 行包含两个数 $s_i, t_i$。$s_i$ 表示通向第 $i$ 座城市的公路的起点，$t_i$ 表示通向第 $i$ 座城市的铁路的起点。如果 $s_i > 0$，那么存在一条从第 $s_i$ 座城市通往第 $i$ 座城市的公路，否则存在一条从第 $-s_i$ 个乡村通往第 $i$ 座城市的公路；$t_i$ 类似地，如果 $t_i > 0$，那么存在一条从第 $t_i$ 座城市通往第 $i$ 座城市的铁路，否则存在一条从第 $-t_i$ 个乡村通往第 $i$ 座城市的铁路。

接下来 $n$ 行，每行描述一个乡村。其中第 $i$ 行包含三个数 $a_i, b_i, c_i$，其意义如题面所示。

输出

输出一行一个整数，表示最优翻修方案的不便利值。

样例

样例输入 1

6
2 3
4 5
-1 -2
-3 -4
-5 -6
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

样例输出 1

54

样例输入 2

9
2 -2
3 -3
4 -4
5 -5
6 -6
7 -7
8 -8
-1 -9
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1

样例输出 2

9
2 -2
3 -3
4 -4
5 -5
6 -6
7 -7
8 -8
-1 -9
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1

样例输入 3

12
2 4
5 3
-7 10
11 9
-1 6
8 7
-6 -10
-9 -4
-12 -5
-2 -3
-8 -11
53 26 491
24 58 190
17 37 356
15 51 997
30 19 398
3 45 27
52 55 838
16 18 931
58 24 212
43 25 198
54 15 172
34 5 524

样例输出 3

5744902

提示

【样例解释 1】

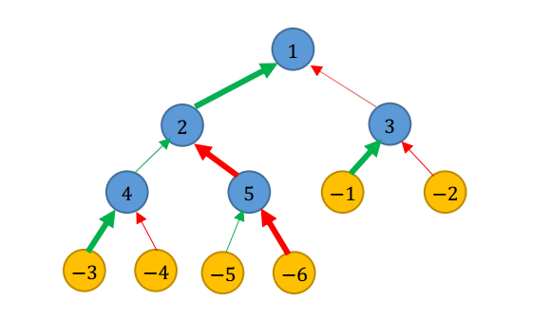
00.PNG

如图所示，我们分别用蓝色、黄色节点表示城市、乡村；用绿色、红色箭头分别表示公路、铁路；用加粗箭头表示翻修的道路。

一种不便利值等于 $54$ 的方法是：翻修通往城市 $2$ 和城市 $5$ 的铁路，以及通往其他城市的公路。用 $\rightarrow$ 和 $\Rightarrow$ 表示公路和铁路，用 $_{*}\rightarrow$ 和 $_{*}\Rightarrow$表示翻修的公路和铁路，那么：

  • 编号为 $1$ 的乡村到达首都的路线为：$−1 _{*}\rightarrow 3 \Rightarrow 1$，经过 $0$ 条未翻修公路和 $1$ 条未翻修铁路，代价为 $3 \times (1 + 0) \times (2 + 1) = 9$；
  • 编号为 $2$ 的乡村到达首都的路线为：$−2 \Rightarrow 3 \Rightarrow 1$，经过 $0$ 条未翻修公路和 $2$ 条未翻修铁路，代价为 $2 \times (1 + 0) \times (3 + 2) = 10$；
  • 编号为 $3$ 的乡村到达首都的路线为：$−3 _{*}\rightarrow 4 \rightarrow 2 _{*}→ 1$，经过 $1$ 条未翻修公路和 $0$ 条未翻修铁路，代价为 $3 \times (2 + 1) \times (1 + 0) = 9$；
  • 编号为 $4$ 的乡村到达首都的路线为：$−4 \Rightarrow 4 \rightarrow 2 {*}\rightarrow 1$，经过 $1$ 条未翻修公路和 $1$ 条未翻修铁路，代价为 $1 \times (2 + 1) \times (3 + 1) = 12$；
  • 编号为 $5$ 的乡村到达首都的路线为：$−5 → 5 _{*}\Rightarrow 2 _{*}\rightarrow 1$，经过 $1$ 条未翻修公路和 $0$ 条未翻修铁路，代价为 $2 \times (3 + 1) \times (1 + 0) = 8$；
  • 编号为 $6$ 的乡村到达首都的路线为：$−6 _{*}\Rightarrow 5 _{*}\Rightarrow 2 _{*}\rightarrow 1$，经过 $0$ 条未翻修公路和 $0$ 条未翻修铁路，代价为 $1 \times (3 + 0) \times (2 + 0) = 6$；

总的不便利值为 $9 + 10 + 9 + 12 + 8 + 6 = 54$。可以证明这是本数据的最优解。

【样例解释 2】

在这个样例中，显然应该翻修所有公路。

【数据规模】

共 $20$ 组数据，编号为 $1 ∼ 20$。

对于编号 $\le 4$ 的数据，$n \le 20$；

对于编号为 $5 \sim 8$ 的数据，$a_i, b_i, c_i \le 5，n \le 50$；

对于编号为 $9 \sim 12$ 的数据，$n \le 2000$；

对于所有的数据，$n \le 20000$，$1 \le a_i, b_i \le 60$，$1 \le c_i \le 10^9$，$s_i, t_i$ 是 $[−n, −1] \cap (i, n − 1]$ 内的整数，任意乡村可以通过不超过 $40$ 条道路到达首都。