平面上的矿区划分成了若干个开发区域。
简单地说，你可以将矿区看成一张连通的平面图，平面图划分为了若干平面块，每个平面块即为一个开发区域，平面块之间的边界必定由若干整点（坐标值为整数的点）和连接这些整点的线段组成。每个开发区域的矿量与该开发区域的面积有关：具体而言，面积为 $s$ 的开发区域的矿量为 $s^2$。
现在有 $m$ 个开采计划。每个开采计划都指定了一个由若干开发区域组成的多边形，一个开采计划的优先度被规定为矿量的总和÷开发区域的面积和；例如，若某开采计划指定两个开发区域，面积分别为 $a$ 和 $b$，则优先度为 $(a^2+b^2)/(a+b)$。由于平面图是按照划分开发区域边界的点和边给出的，因此每个开采计划也只说明了其指定多边形的边界，并未详细指明是哪些开发区域（但很明显，只要给出了多边形的边界就可以求出是些开发区域）。
你的任务是求出每个开采计划的优先度。为了避免精度问题，你的答案必须按照分数的格式输出，即求出分子和分母，且必须是最简形式（分子和分母都为整数，而且都消除了最大公约数；例如，若矿量总和是 $1.5$，面积和是 $2$，那么分子应为 $3$，分母应为 $4$；又如，若矿量和是 $2$，面积和是 $4$，那么分子应为$1$，分母应为 $2$）。
由于某些原因，你必须依次对每个开采计划求解（即下一个开采计划会按一定格式加密，加密的方式与上一个开采计划的答案有关）。具体的加密方式见输入格式。
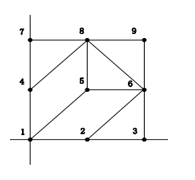
第一行三个正整数 $n, m, k$，分别描述平面图中的点和边，以及开采计划的个数。
接下来 $n$ 行，第 $i$ 行 ($i = 1, 2, \cdots , n$) 有两个整数 $x_i, y_i$, 表示点 $i$ 的坐标为 $(x_i, y_i)$。
接下来 $m$ 行，第 $i$ 行有两个正整数 $a, b$，表示点 $a$ 和 $b$ 之间有一条边。
接下来一行若干个整数，依次描述每个开采计划。每个开采计划的第一个数 $c$ 指出该开采计划由开发区域组成的多边形边界上的点的个数为 $d=(c+P) \bmod n \mathrel{+} 1$；接下来 $d$ 个整数，按逆时针方向描述边界上的每一个点：设其中第 $i$ 个数为 $z_i$，则第 $i$ 个点的编号为 $(z_i+P)\bmod n \mathrel{+} 1$。其中 $P$ 是上一个开采计划的答案中分子的值；对于第 $1$ 个开采计划，$P = 0$。
对于每个开采计划，输出一行两个正整数，分别描述分子和分母。
Comet OJ9 14 5
0 0
1 0
2 0
0 1
1 1
2 1
0 2
1 2
2 2
1 2
2 3
5 6
7 8
8 9
1 4
4 7
5 8
3 6
6 9
4 8
1 5
2 6
6 8
3 3 0 4 7 1 3 4 6 4 8 0 4 3 6 2 3 8 0 4 6 2 5 0 4 5 7 6 31 1
1 2
1 1
9 10
3 4【样例解释】
输入文件给出的 $9$ 个点和 $14$ 条边描述的平面图如下所示：
第一个开采计划，输入的第一个值为 $3$，所以该开采计划对应的多边形有 $(3+0)\bmod 8 \mathrel{+} 1 = 4$ 个点，将接下的四个数 $3, 0, 4, 7$，分别代入 $(z_i+0)\bmod n \mathrel{+} 1$ 得到四个点的编号为 $4, 1, 5, 8$。计算出第一个开采计划的分子为 $1$，分母为 $1$。
类似地，可计算出余下开采计划的多边形的点数和点的编号：第二个开采计划对应的多边形有三个点，编号分别为 $5, 6, 8$。第三个开采计划对应的多边形有六个点，编号分别为 $1, 2, 6, 5, 8, 4$。第四个开采计划对应的多边形有五个点，编号分别为 $1, 2, 6, 8, 4$。第五个开采计划对应的多边形有六个点，编号分别为 $1, 5, 6, 8, 7, 4$。
【数据规模】
对于 $100 \%$ 的数据，$n, k \leq 2 \times 10^5, \ m \leq 3n-6, \ |x_i|, |y_i| \leq 3×10^4$。所有开采计划的 $d$ 之和不超过 $2 \times 10^6$。保证任何开采计划都包含至少一个开发区域，且这些开发区域构成一个连通块。保证所有开发区域的矿量和不超过 $2^{63}-1$。保证平面图中没有多余的点和边。保证数据合法。由于输入数据量较大，建议使用读入优化。