第一行三个整数:$N, M, Q$,以空格隔开,$N$ 表示模板树结点数,$M$ 表示第 (2) 中的循环操作的次数,$Q$ 表示询问数量。
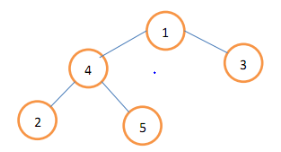
接下来 $N-1$ 行,每行两个整数 $\text{fr}, \text{to}$,表示模板树中的一条树边。
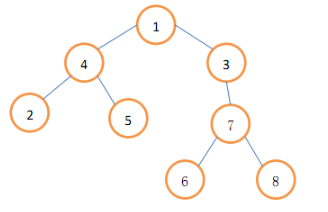
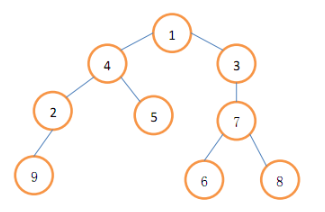
再接下来 $M$ 行,每行两个整数 $x, \text{to}$,表示将模板树中 $x$ 为根的子树复制到大树中成为结点 $\text{to}$ 的子树的一次操作。
再接下来 $Q$ 行,每行两个整数 $\text{fr}, \text{to}$,表示询问大树中结点 $\text{fr}$ 和 $\text{to}$ 之间的距离是多少。