C0715 [BJOI2016]水晶

不用惊慌，今天的题都不是小强出的。——融入了无数心血的作品，现在却不得不亲手毁掉，难以体会他的心情啊。——那也是没有办法的事情，能量共振不消除的话……望着已经被装上炸药的水晶，02放下了望远镜，看向了手中的共振分析报告。还是会有一些水晶，幸存下来的……也许吧。

地图由密铺的六边形单元组成，每个单元与其他六个单元相邻。为了方便起见，我们用坐标 $(x,y,z)$ 描述一个单元的位置，表示从原点开始按如图所示的 $x,y,z$ 方向各走若干步之后到达的地方。有可能有两个坐标描述同一个单元，比如 $(1,1,1)$ 和 $(0,0,0)$ 描述的都是原点。

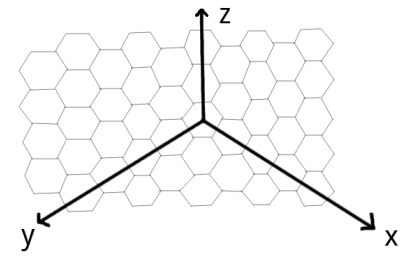
显然 $(x,y,z)$ 单元和 $(x+1, y,z)，(x-1,y,z)，(x,y+1,z)，(x,y-1,z)，(x, y, z+1)，(x,y, z-1)$ 相邻。有 $N$ 块水晶位于地图的单元内，第i块水晶位于坐标 $(x_i, y_i, z_i)$ 所表示的单元中，并拥有 $c_i$ 的价值。每个单元内部可能会有多块水晶。地图中，有一些单元安装有能量源。如下图，任何满足 $x+y+z$ 是 $3$ 的整数倍的坐标所描述的单元内都安装有能量源。

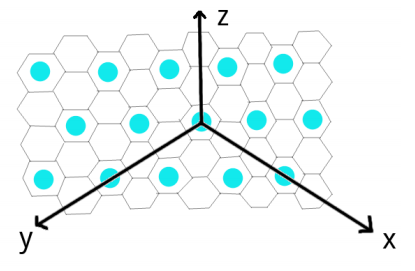
有能量源的单元中的水晶价值将会额外增加 $10\%$。如果三块水晶所在的单元满足特定排列，那么它们将会引发共振。

共振分两种，$a$ 共振和 $b$ 共振。

$a$ 共振：如果三块水晶所在的单元两两相邻地排成一个三角形，那么会引起 $a$ 共振。

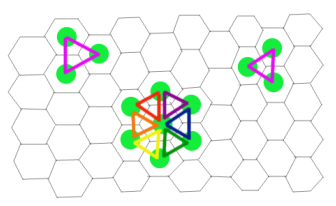
图中每一个三角形表示这三个单元各有一块水晶将会发生一个 $a$ 共振。

$b$ 共振：如果三块水晶所在的单元依次相邻地排成一条长度为 $2$ 的直线段，且正中间的单元恰好有能量源，那么会引起 $b$ 共振。

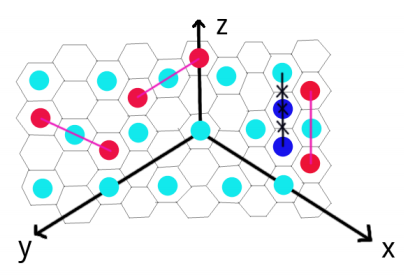
图中粉红色线段表示这三个单元各有一块水晶将会发生一个 $b$ 共振，黑色线段表示即使这三个单元有水晶也不会发生 $b$ 共振。现在你要炸掉一部分水晶，使得任何共振都不会发生的前提下，剩余水晶的价值总和最大。

样例输入 1

4
0 0 0 11
1 0 0 5
0 1 0 7
0 0 -1 13

样例输出 1

25.1