Comet OJ

C0704 [BJOI2013]分数

内存限制：256 MB 时间限制：1000 ms

题目描述

出题最困难的地方在于调控分数。题目必须要让选手之间的实力差异通过分数体现出来。而参加考试的选手的能力水平分布严重影响了题目的得分分布。适合一个省份的题目换到另一个省份里可能就瞬间变得没有意义。这里面有一个十分微妙的关系。为了更好的把握题目的难度，小强建立了一个模型。每个选手的实力都是一个 $0$ 到 $100$ 之间的实数。小强可以掌控一个题目的“难度”和“区分度”。一个选手的得分是：

实际分数 = $\frac{100}{1+exp(难度-区分度\times实力)}$

其中，$exp$ 是指数函数。理想情况下，$N$ 个选手 $(N \ge 3)$ 的理想分数应当形成一个首项 $100$，末项为 $0$ 的等差数列（我们把实力最强的选手排在最前面）。定义一个题目的分数偏差为：

$\sum_{对所有学生}(理想分数 \times \ln(\frac{100}{实际分数})+(100-理想分数) \times \ln(\frac{100}{100-实际分数}))$

其中，$\ln$ 是自然对数。现在，你要计算：对于给定的 $N$ 个选手的实力，分数偏差的最小值是多少？

输入格式

第一行包含两个正整数 $N$ 和 $P$，表示选手的个数以及精度要求。

接下来的 $N$ 行，每行包含一个 $0$ 到 $100$（闭区间）内的整数。

输出

输出一个实数，取 $P$ 位有效数字，下取整。

样例

样例输入 1

5 4
100
20
15
10
8

样例输出 1

195.2

提示

【样例解释】

很显然，这个队伍里面有一个神牛和一群水人。出题的时候应当把精力放在如何区分水人中谁更水，而不是牛人中谁更牛上。

最优的情况下，难度是 $4.662016$，区分度是 $0.299386$，此时实际得分是：

$99.999999，79.013041，45.729992，15.86770，9.389952$

下面这个图展示了理想得分、实际得分关于实力的函数。

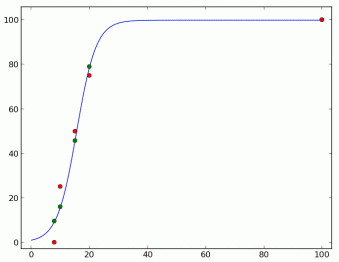
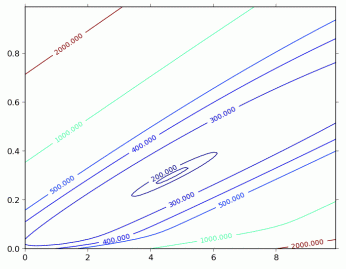
image.png

作为对你的一个额外的提示，下面这个图是分数误差关于难度-区分度的图像。可以看到，这里只有一个极值点。

image.png

【数据规模和约定】

一共有 $10$ 个测试点，$P$ 的值依次是 $1$ 到 $10$。

对 100% 的数据，$N≤20$。