Comet OJ

C0593 [ZJOI2018]树

内存限制：512 MB 时间限制：3000 ms

题目描述

九条可怜是一个热爱出题的女孩子。

虽然出题本身是一件非常有趣的事情，但是要把题目给出成正式比赛，就不是那么有趣了：造数据总是一件让人心力憔悴的事情。

在 ZJOI2018 Day 1 中，可怜出了一道和树相关的非常有趣的题，她打算采用一种常用的方式随机生成一棵 $n$ 个节点的有根树：

  • 节点 $1$ 作为树的根。
  • 对于 $i \in [2,n]$，独立地从 $[1, i)$ 中等概率随机选取一个节点作为 $i$ 的父亲。

可怜不是很想考虑这样随机出来的数据能不能卡掉暴力，毕竟乱搞也是 OI 比赛的一部分。

可怜比较在意的是题目的区分度，以及是不是所有可能的分数都出现了。因此，可怜希望任何两个测试点的树是有区别的：这样就可能会有错误的程序能只通过其中一个点。

因此，可怜想要计算，通过上面的方法独立的随机生成 $k$ 棵 $n$ 个节点的有根树 $T_1$ 至 $T_k$，他们两两同构的概率是多少。

两棵 $n$ 个节点的有根树 $T_1$ 和 $T_2$ 同构当且仅当存在长度为 $n$ 的排列 $p$，满足 $p_1 = 1$，且对于 $\forall i \in [2, n]$，若 $i$ 在 $T_1$ 的父亲是 $f$，则 $p_i$ 在 $T_2$ 的父亲是 $p_f$。

输入格式

第一行输入三个整数 $n, k, p$，表示节点个数，树的个数以及模数。输入保证 $10^8 \leq p \leq 10^9$ 且 $p$ 是质数。

输出

输出一行一个整数，表示答案对 $p$ 取模后的值。即如果答案的最简分数表示为 $\frac{a}{b}$，输出 $a \times b^{−1} \bmod p$。

样例

样例输入 1

2 2 998244353
3 2 998244353
4 2 998244353
10 2 998244353
50 233 998244353

样例输出 1

1
499122177
332748118
113919852
634280054

提示

【样例解释】

样例中有五组不同的数据，所以输入格式略有不同。在实际的测试数据中，输入只有一行。

在第一组数据中，能够生成的树是唯一的，因此生成的两棵树必定相同。

在第二组数据中，能够生成的树只有两种，他们是不同构的。因此生成的两棵树同构的概率为 $\displaystyle\frac{1}{2}$，在模 $998244353$ 意义下为 $499122177$。

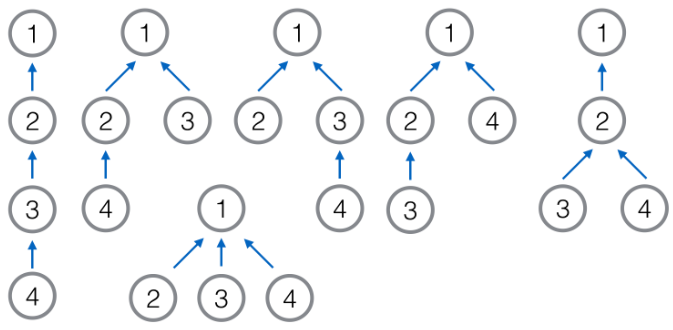
在第三组数据中，能够生成的树有 $6$ 种，如下图所示。其中第二、三、四棵(第一排中间三棵)是同构的，其余两两不同构。因此生成的两棵树同构的概率为 $\displaystyle\frac{1}{3}$，在模 $998244353$ 意义下为 $332748118$。

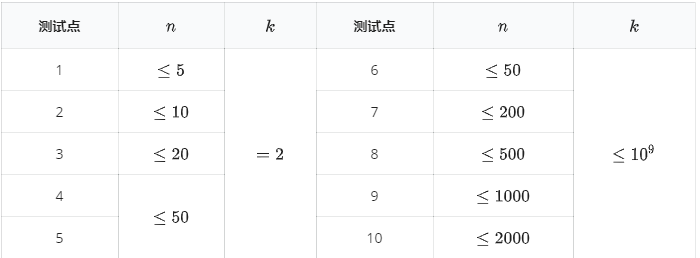
image.png

【数据范围与提示】

image.png

对于 $100%$ 的数据，保证$p$是质数且 $10^8 \le p \le 10^9$。