首先介绍一下 Kakuro(カックロ) 这个游戏。
游戏规则为：
上方为一个 Kakuro 游戏，下方为这个游戏的唯一解。
我们称一开始给出的数字为线索，称需要填入数字的地方为空格。如果一个格子包含线索那么就不需要填入数字。我们约定所有的谜题都非空，即至少有一个空格需要被填入。
注意：在以下题目中的游戏规则可能会有所不同，请认真阅读在每个题目下的规则。
【题目详情】
游戏规则：
Apia 给了 Rimbaud 一个 Kakuro 谜题。心不灵手不巧的 Rimbaud 根本不会做 Kakuro，所以只在空格里面填上了一些随机的数字，称这个为一个局面，即包含了谜题一开始给出的线索和后面填入的数字。现在 Rimbaud 希望能修改这个局面使得她的答案是一个合法解。这个局面中有些数字（包括一开始的给出线索和后面填入的数字）是可以修改的。每个数字都有个特定的代价，将这个数字加 $1$ 或者减 $1$ 都得付出这个数字对应的代价。注意对于一组合法解，必须满足游戏规则，也就是空格中填的数字必须是正整数并且满足和的条件，但是不要求不重复。
Rimbaud 希望用最少的代价让这个局面变得合法，如果不可能那么输出 $-1$。
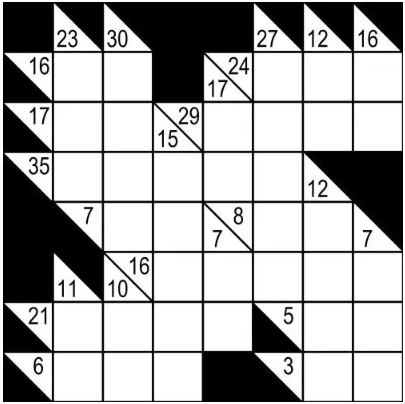
第一行，两个正整数表示 $n,m$ 表示这个游戏的行和列。
接下来 $n$ 行，每行包含 $m$ 个 $0$ 到 $4$ 的数字，第 $i$ 行第 $j$ 列表示第 $i$ 行第 $j$ 列格子的种类。
输入保证这个从格式上来说一定是个合法的 Kakuro 谜题，即每一段连续的空格的左边或者上面的格子包含线索。
接下来 $n$ 行，每行包含若干个正整数，按从左往右的顺序给出初始局面中的每个数字。特别地如果这个格子的种类为 $3$，那么先给出左下角的线索，再给出右上角的线索。
接下来 $n$ 行，每行包含若干个整数，按从左往右的顺序给出初始局面中的每个数字对应的代价。如果代价为 $-1$ 表示这个格子不能修改，否则代价为非负整数。注意 $3$ 号格子的两个线索有着两个不同的代价。
一个整数表示最小的代价，如果不可能输出 $-1$。
Comet OJ8 8
0 1 1 0 0 1 1 1
2 4 4 0 3 4 4 4
2 4 4 3 4 4 4 4
2 4 4 4 4 4 1 0
0 2 4 4 3 4 4 1
0 1 3 4 4 4 4 4
2 4 4 4 4 2 4 4
2 4 4 4 0 2 4 4
23 30 27 12 16
16 9 7 17 24 8 7 9
17 8 9 15 29 8 9 5 7
35 6 8 5 9 7 12
7 6 1 7 8 2 6 7
11 10 16 4 6 1 3 2
21 8 9 3 1 5 1 4
6 3 1 2 3 2 1
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -105 5
0 1 1 1 1
2 4 4 4 4
2 4 4 3 4
2 4 4 4 4
2 4 4 4 4
16 8 6 8
4 4 9 5 4
12 8 4 19 10 4
14 2 3 3 6
1 7 9 4 5
17 5 10 13
11 15 16 4 14
20 20 15 5 16 3
4 3 19 2 4
19 19 13 15 20822【样例 1 解释】
样例 $1$ 给出了上面的谜题的输入，请在做题前阅读样例 $1$ 确保你理解了输入格式。
【数据范围与提示】
对于 $5\%$ 的数据，保证所有的代价都为 $-1$。
对于 $20\%$ 的数据，保证所有空格中的数字代价都为 $-1$。
对于另外 $30\%$ 的数据，保证所有代表线索的数字的代价都为 $-1$。
对于另外 $20\%$ 的数据，保证只有第一行第一列包含线索，剩下的地方全都是空格。
对于 $100\%$ 的数据，保证 $3\le n, m\le 30$，保证初始局面中的每个数字不超过 $10^6$，保证每个数字的代价不超过$10^6$。