Comet OJ

C0522 [CEOI2009Day2] tri

内存限制：256 MB 时间限制：2000 ms

题目描述

You are given $K$ points with positive integer coordinates. You are also given $M$ triangles, each of them having one vertex in the origin and the other $2$ vertices with non-negative integer coordinates.

You are asked to determine for each triangle whether it has at least one of the $K$ given points inside. (None of the $K$ points are on any edge of any triangle.)

输入格式

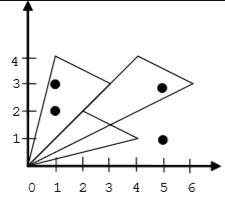
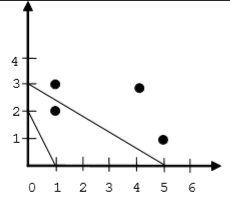
The first line of the input will contain $K$ and $M$. The following $K$ lines will contain $2$ positive integers $x$ $y$ separated by one space that represent the coordinates of each point. The next $M$ lines have $4$ non-negative integers separated by one space, $(x1,y1)$ and $(x2, y2)$, that represent the other $2$ vertices of each triangle, except the origin.

输出

The output should contain exactly $M$ lines. The $k$-th line should contain the character $Y$ if the $k$-th triangle (in the order of the input) contains at least one point inside it, or $N$ otherwise.

样例

样例输入 1

4 3
1 2
1 3
5 1
5 3
1 4 3 3
2 2 4 1
4 4 6 3

样例输出 1

Y
N
Y

样例输入 2

4 2
1 2
1 3
5 1
4 3
0 2 1 0
0 3 5 0

样例输出 2

N
Y

提示

Explanation

sample 1:

image.png

sample 2:

image.png

Constraints

$1 ≤ K,M ≤ 100 000$

$1 ≤$ each coordinate of the $K$ points $≤ 10^9$

$0 ≤$ each coordinate of the triangle vertices $≤ 10^9$

Triangles are not degenerate (they all have nonzero area).

In 50% of the test cases, all triangles have vertices with coordinates $x_1=0$ and $y_2=0$. That is, one edge of the triangle is on the $x$-axis, and another is on the $y$-axis.