One morning, fruit farmer Fred visits his apple trees and notices that one of them was cut overnight. This means a loss of 111€ – the money he can make from the apples of a tree on average. In order to prevent further losses, he decides to erect a fence on his plantation.
The fence consists of posts connected by wire. The fence posts can only be placed at a given set of pre-drilled holes. While Fred can get wire for free, he needs to buy the fence posts for 20€ each. So it might not always be worth or even possible to fence in all of his trees.
The plantation is square and $1000×1000$ $m^2$ large. In bird’s eye view, the lower left corner has coordinates $(0,0)$, the upper right $(1000,1000)$.
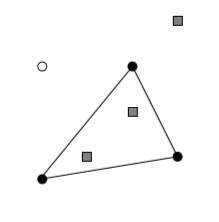
In this example there are four pre-drilled holes (circles) and three trees (squares). It is optimal to buy three fence posts and put them into selected holes (filled circles), to connect them by wire (lines), and to leave the upper left hole empty. The cost of erecting the fence is $3·20$€ + $1·111$€ = 171€since three posts were bought and one tree could not be fenced in (which means a loss of that tree’s harvest).
Write a program that reads the positions of the pre-drilled holes and the trees on Fred’s plantation and outputs the minimum cost of erecting a fence or erecting no fence at all. You can neglect the actual shape of the trees and calculate with their positions only.
The first line contains two integers $N$ and $M (3≤ N ≤100,1≤ M ≤100)$. $N$ is the number of pre-drilled holes, and $M$ is the number of trees. This line is followed by $N$ lines that describe the positions of the holes, and then by $M$ lines that describe the positions of the trees. All positions are given as pairs of integers $x$ $y4 on one line $(0 ≤ x,y ≤ 1000)$. You can expect that no two positions (of holes and trees) coincide and that no three positions are colinear.
Output a single line containing one integer: Fred’s minimum cost. In case Fred buys $P$ posts and fails to fence in $T$ trees, his cost are $20P +111T$.
Comet OJ4 3
800 300
200 200
200 700
600 700
400 300
600 500
800 900171This sample corresponds to the picture above.