Comet OJ

C0477 [APIO2016-B]烟花表演

内存限制：256 MB 时间限制：1000 ms

题目描述

烟花表演是最引人注目的节日活动之一。在表演中，所有的烟花必须同时爆炸。为了确保安全，烟花被安置在远离开关的位置上，通过一些导火索与开关相连。导火索的连接方式形成一棵树，烟花是树叶，如图所示。火花从开关出发，沿导火索移动。每当火花抵达一个分叉点时，它会扩散到与之相连的所有导火索，继续燃烧。导火索燃烧的速度是一个固定常数。图中展示了六枚烟花 $\{ E_1​,E_2​,...,E_6 \}$ 的连线布局，以及每根导火索的长度。图中还标注了当在时刻0从开关点燃火花时，每一发烟花的爆炸时间。

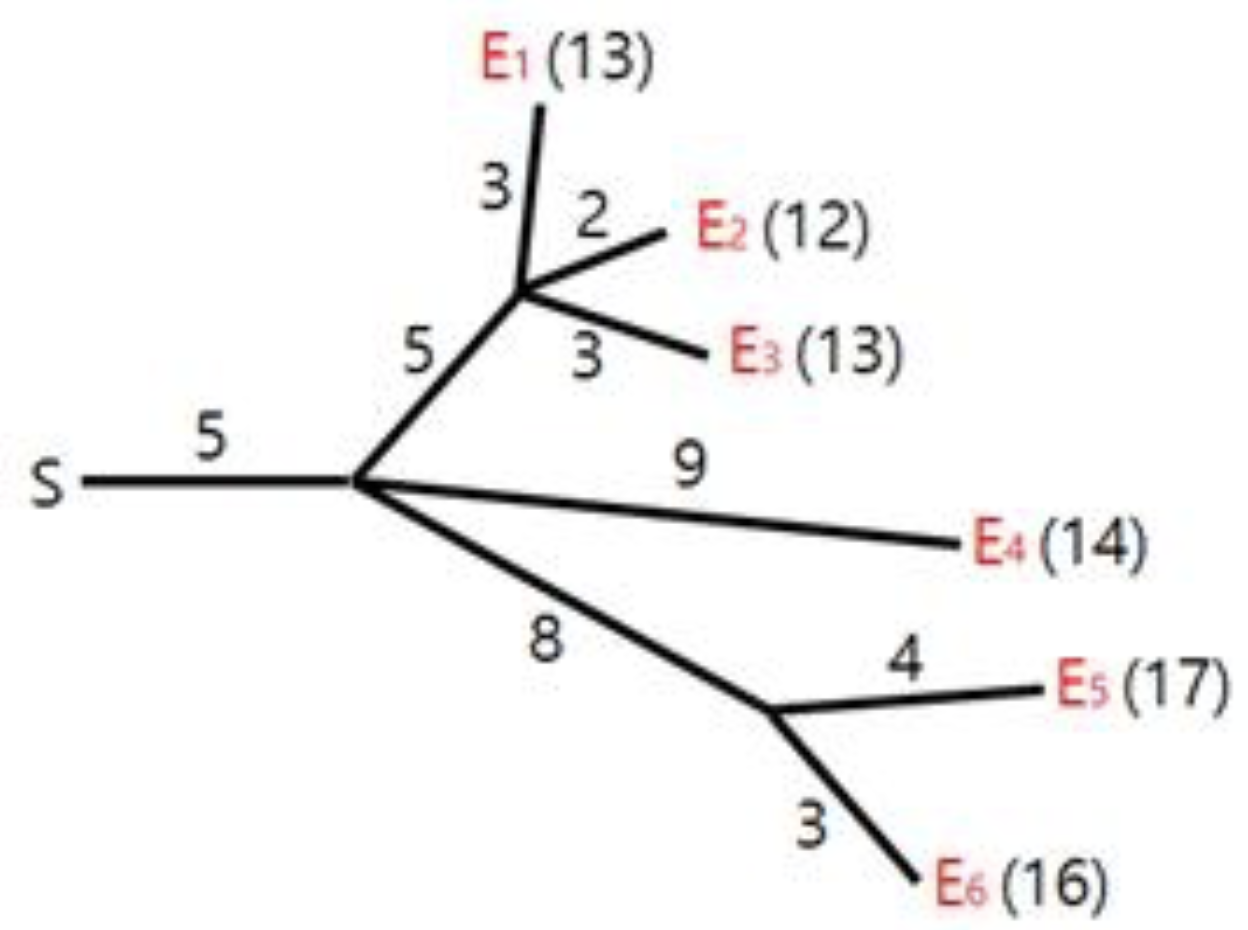
屏幕快照 2019-06-24 上午10.02.16.png

Hyunmin 为烟花表演设计了导火索的连线布局。不幸的是，在他设计的布局中，烟花不一定同时爆炸。我们希望修改一些导火索的长度，让所有烟花在同一时刻爆炸。例如，为了让上图中的所有烟花在时刻 13 爆炸，我们可以像下图中左边那样调整导火索长度。类似地，为了让上图中的所有烟花在时刻 14 爆炸，我们可以像下图中右边那样调整长度。

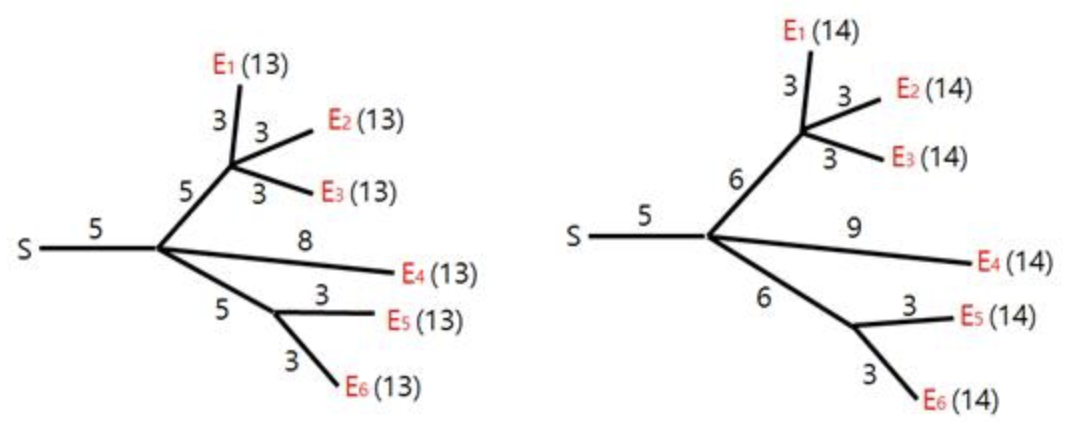
屏幕快照 2019-06-24 上午10.03.57.png

修改导火索长度的代价等于修改前后长度之差的绝对值。例如，将上面一幅图中布局修改为下面一幅图，左边布局的总代价为 6，右边布局的总代价为 5。

导火索的长度可以被减为 0，同时保持连通性不变。

给定一个导火索的连线布局，你需要编写一个程序，去调整导火索长度，让所有的烟花在同一时刻爆炸，并使得代价最小。

输入格式

所有的输入均为正整数。令 $N$ 代表分叉点的数量，$M$ 代表烟花的数量。分叉点从 $1$ 到 $N$ 编号，编号为 $1$ 的分叉点是开关。烟花从 $N+1$ 到 $N+M$ 编号。

输入格式如下：

输入第一行为 $N,M$。后面 $N+M−1$ 行，第 $i$ 行两个整数 $P_{i+1},C_{i+1}$。其中 $P_i$​ 满足 $1≤P_i<i$，代表和分叉点或烟花ii相连的分叉点。$C_i$​ 代表连接它们的导火索长度（$1≤C_i≤10^9$）除开关外，每个分叉点和多于 1 条导火索相连，而每发烟花恰好与 1 条导火索相连。

输出

输出调整导火索长度，让所有烟花同时爆炸，所需要的最小代价。

样例

样例输入 1

4 6
1 5
2 5
2 8
3 3
3 2
3 3
2 9
4 4
4 3

样例输出 1

5

提示

【数据规模】（comet 不支持APIO评分方式）

子任务 1（7 分）：$N=1$，$1≤M≤100$。

子任务 2（19 分）：$1≤M≤300$，且开关到任一烟花的距离不超过300。

子任务 3（29 分）：$1≤M≤5000$。

子任务 4（45 分）：$1≤M≤300000$。