Comet OJ

C0473 [APIO2015-C]八邻旁之桥

内存限制：256 MB 时间限制：2000 ms

题目描述

一条东西走向的穆西河将巴邻旁市一分为二，分割成了区域 $A$ 和区域 $B$。

每一块区域沿着河岸都建了恰好 $1000000001$ 栋的建筑，每条岸边的建筑都从 $0$ 编号到 $1000000000$。相邻的每对建筑相隔 $1$ 个单位距离，河的宽度也是 $1$ 个单位长度。区域 $A$ 中的 $i$ 号建筑物恰好与区域 $B$ 中的 $i$ 号建筑物隔河相对。

城市中有 $N$ 个居民。第 $i$ 个居民的房子在区域 $P_i$ 的 $S_i$​ 号建筑上，同时他的办公室坐落在 $Q_i$​ 区域的 $T_i$​ 号建筑上。一个居民的房子和办公室可能分布在河的两岸，这样他就必须要搭乘船只才能从家中去往办公室，这种情况让很多人都觉得不方便。为了使居民们可以开车去工作，政府决定建造不超过$K$座横跨河流的大桥。由于技术上的原因，每一座桥必须刚好连接河的两岸，桥梁必须严格垂直于河流，并且桥与桥之间不能相交。

当政府建造最多 $K$ 座桥之后，设 $D_i$​ 表示第 $i$ 个居民此时开车从家里到办公室的最短距离。请帮助政府建造桥梁，使得 $D_1+D_2+⋯+D_N$​ 最小。

输入格式

输入的第一行包含两个正整数 $K$ 和 $N$，分别表示桥的上限数量和居民的数量。

接下来 $N$ 行，每一行包含四个参数：$P_i,S_i,Q_i$ 和 $T_i$​，表示第 $i$ 个居民的房子在区域 $P_i$​ 的 $S_i$​ 号建筑上，且他的办公室位于 $Q_i$ ​区域的 $T_i$​ 号建筑上。

输出

输出仅为一行，包含一个整数，表示 $D_1+D_2+⋯+D_N$ ​的最小值。

样例

样例输入 1

1 5
B 0 A 4
B 1 B 3
A 5 B 7
B 2 A 6
B 1 A 7

样例输出 1

24

样例输入 2

2 5
B 0 A 4
B 1 B 3
A 5 B 7
B 2 A 6
B 1 A 7

样例输出 2

22

提示

【样例说明】

下图是两个样例输入的图示说明：

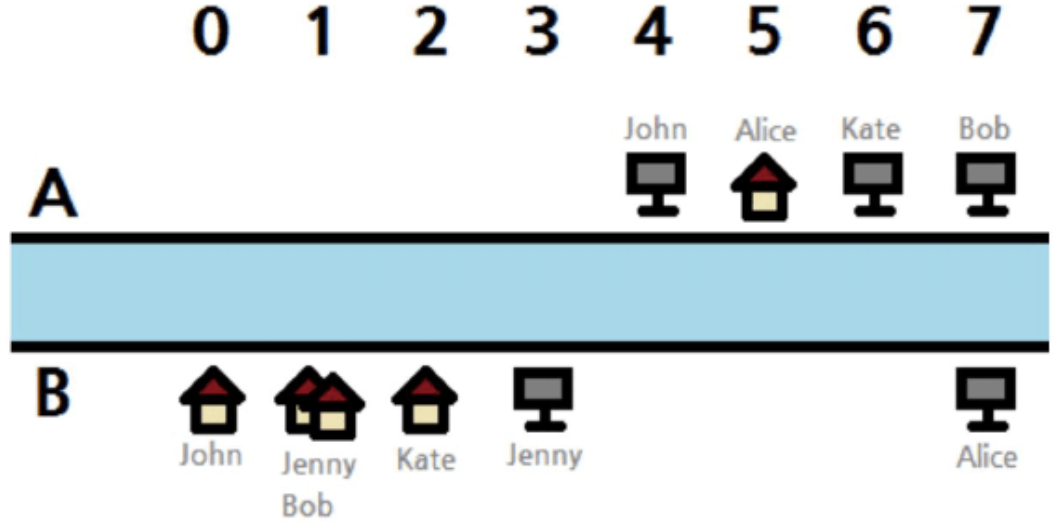
屏幕快照 2019-06-19 下午6.35.12.png

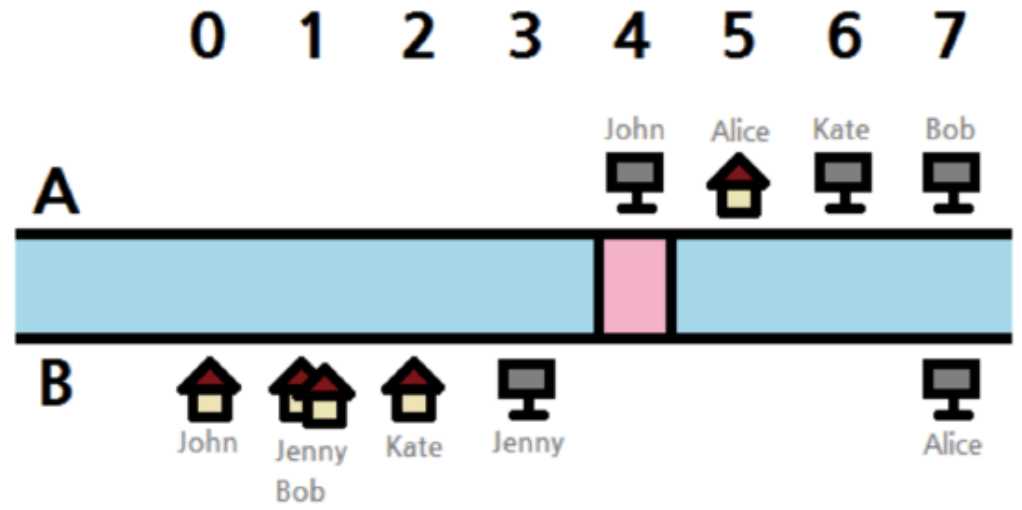
下面是样例 1 可能的一组最优方案，粉色的区域表示一座桥。

屏幕快照 2019-06-19 下午6.36.15.png

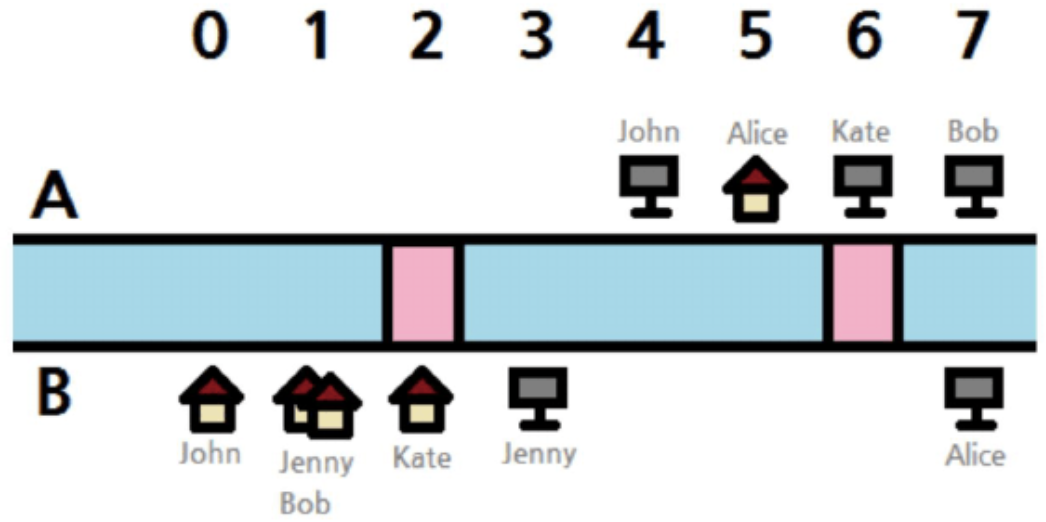
下面是样例 2 的一组可能是最优方案。

屏幕快照 2019-06-19 下午6.37.00.png

【数据规模和约定】

共有五部分数据（或称5个子任务）。所有数据都保证：$0 \le S_i,T_i \le 1000000000$，$P_i$ 和 $Q_i$ 为字符 $A$ 和 $B$ 中的一个，同一栋建筑内可能有超过 1 间房子或办公室（或二者的组合，即房子或办公室同时大于等于 1）。

第 1 部分数据（测试点 1-11）占8分，数据范围满足：$K=1,1 \le N \le 1000$

第 2 部分数据（测试点 12-21）占14分，数据范围满足：$K=1,1 \le N \le 100000$

第 3 部分数据（测试点 22-33）占9分，数据范围满足：$K=2,1 \le N \le 100$

第 4 部分数据（测试点 34-45）占32分，数据范围满足：$K=2,1 \le N \le 1000$

第 5 部分数据（测试点 46-57）占37分，数据范围满足：$K=2,1 \le N \le 100000$