第一行三个用空格隔开的整数 $n,y,op$。 如果 $op=0$,则接下来 $2×(n−1)$ 行,前 $(n−1)$ 行每描述一条蓝色绳子,接下来 $(n−1)$ 行每行描述一条红色绳子。
如果 $op=1$,则接下来 $(n−1)$ 行,每行描述一条蓝色绳子。
如果 $op=2$,则接下来没有输入。
描述绳子的各行将包含两个用空格隔开的整数,分别表示被这条绳子连接的两只鼠的编号。鼠的编号是从 $1$ 开始的。
白兔喜欢树。
白云喜欢数数。
有 $n$ 只鼠,白兔用 $n−1$ 根蓝色绳子把它们连成了一棵树,每根蓝色绳子连着两只鼠,白云用 $n−1$ 根红色绳子把它们连成了一棵树,每根红色绳子连接着两只鼠。
白云要给予每只鼠一个数。这个数可以是 $[1,y]$ 中的任意一个整数。
白兔给了白云一个要求:对于两只鼠 $p,q$,若存在一条连接这两只鼠的路径同时属于这两棵树,则 $p$ 和 $q$ 必须被给予相同的整数。存在一条路径同时属于这两棵树指的是:存在一个序列 $(a_1=p,a_2,⋯,a_m=q)$,使得:对于所有 $i \in [1,m−1]$,都有 $a_i$ 和 $a_{i+1}$ 既有一根红色绳子直接相连也有一根蓝色绳子直接相连。
白云想知道,她有多少种给予数的方案呢?
鼠在不停地挣扎,想要摆脱绳子的束缚。白云还没有思考出来,鼠便把红色绳子都咬断了。
白兔有些气恼,但是他还是想要知道答案。他便问白云:对于所有红色绳子的连接方案,答案的总和(即求所有红色绳子连接方案的给予数方案之和)是多少?
鼠在不停地挣扎,想要摆脱绳子的束缚。白云还没有思考出来,鼠便把蓝色绳子也咬断了。
白兔有些气恼,但是他还是想要知道答案。他便问白云:对于所有红色和蓝色绳子的连接方案,答案的总和(即求所有红色和蓝色绳子连接方案的给予数方案之和)是多少?两个方案不同当且仅当存在至少一对鼠,在两种方案中,这两只鼠之间直接连接的绳子不同(两只鼠之间连接绳子的可能性有 4 种:没有绳子直接连接,只有红色绳子直接连接,只有蓝色绳子直接连接,两种颜色的绳子均直接连接)。
白云哭了。
本题包含三个问题:
提示:$n$ 个节点的树一共有 $n^{n−2}$ 种。
在不同的测试点中,你将可能需要回答不同的问题。我们将用 $op$ 来指代你需要回答的问题编号(对应上述 0、 1、 2)。
由于答案可能很大,因此你只需要输出答案对 $998,244,353$ 取模的结果即可。
第一行三个用空格隔开的整数 $n,y,op$。 如果 $op=0$,则接下来 $2×(n−1)$ 行,前 $(n−1)$ 行每描述一条蓝色绳子,接下来 $(n−1)$ 行每行描述一条红色绳子。
如果 $op=1$,则接下来 $(n−1)$ 行,每行描述一条蓝色绳子。
如果 $op=2$,则接下来没有输入。
描述绳子的各行将包含两个用空格隔开的整数,分别表示被这条绳子连接的两只鼠的编号。鼠的编号是从 $1$ 开始的。
输出一个整数,表示答案对 $998,244,353$ 取模的结果。
3 2 0
1 2
2 3
1 2
2 323 2 1
1 2
2 323 2 230【样例1说明】
两棵树相同,所以任意两个点都必须被给予相同的数,方案数为 $2$。
【样例2说明】
红树共有三种可能的情况:
综上,问题 1 的答案为 $2+4+4=10$。
【样例3说明】
蓝树一共有三种可能的情况。不难发现,对于蓝树的每一种情况,求得的问题 1 的答案都是 $10$。所以答案为 $10×3=30$。
【数据规模】
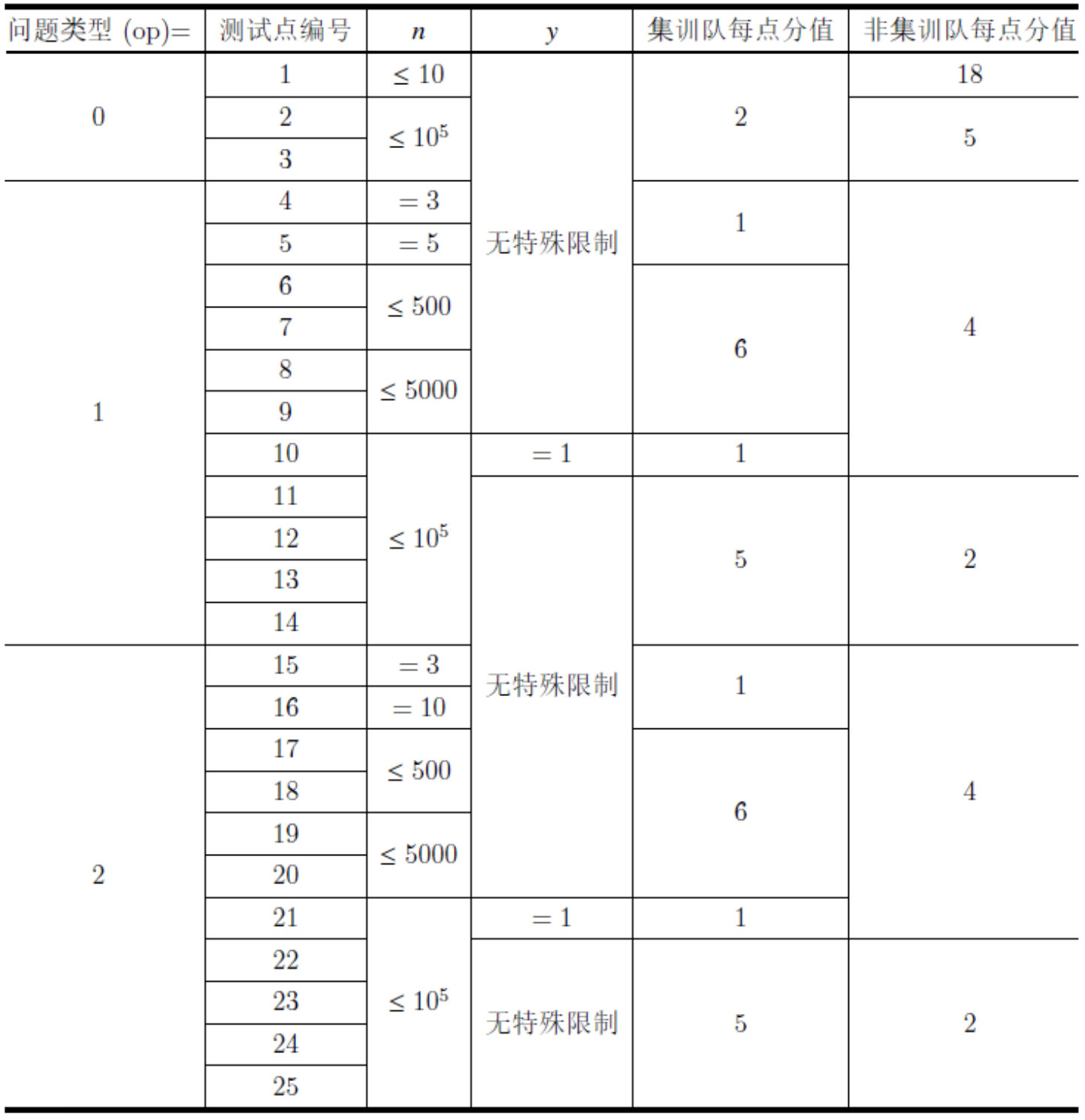
所有测试点均满足 $3 \times 10^5, 1 \le y \le 998244353, op \in \{0, 1, 2\}$