[WC2009-A]最短路问题

一个 $6 \times n$ 的方格，初始每个格子有一个非负权值。有如下两种操作形式：

改变一个格子的权值（改变以后仍然非负）；
求两个格子之间的最短路的权值。

任意格子 P 的坐标 $(x_p,y_p)$ 满足 $1 \le x_p \le 6, 1 \le y_p \le n$。格子 $P$ 和 $Q$ 的曼哈顿距离定义为 $|x_P-x_Q|+|y_P-y_Q|$。一个有序方格序列 $(p_1,p_2,...,p_n)$，若满足任意 $p_i$ 和 $p_{i+1}$ 的曼哈顿距离为 1，则称该序列为一条从 $p_1$ 到 $p_n$ 的路径，其权值为 $d(p_1)+d(p_2)+...+d(p_n)$，其中 $d(P)$ 表示格子 $P$ 的权值。两个格子 $P$ 和 $Q$ 之间的最短路定义为从 $P$ 到 $Q$ 权值最小的路径。

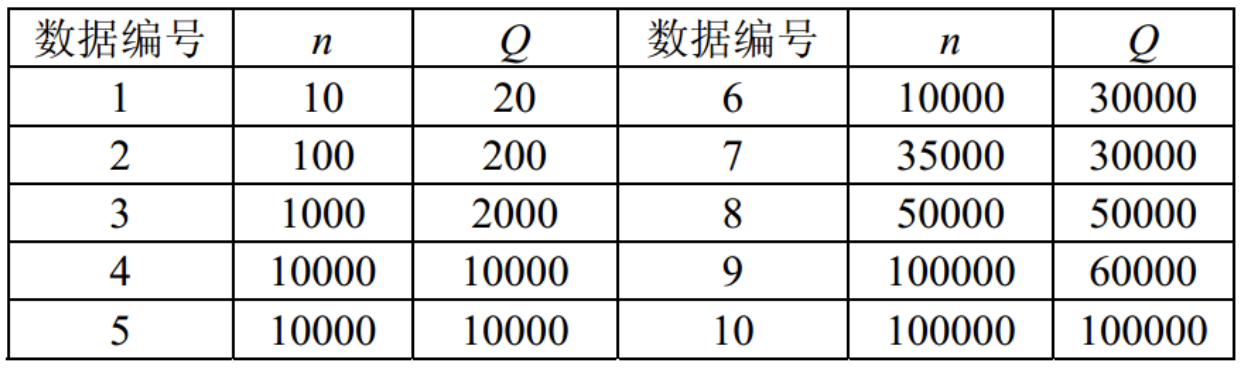
第一行一个整数 $n$。接下来 $6$ 行，每行 $n$ 个整数，第 $i+1$ 行第 $j$ 个整数表示初始格子 $(i,j)$ 的权值。接下来是一个整数 $Q$，后面的 $Q$ 行，每行描述一个操作。输入的操作有以下两种形式：

操作1："1 x y c"（不含双引号）。表示将格子 $(x,y)$ 的权值改成 $c(1 \le x \le 6, 1 \le y \le n, 0 \le c \le 10000)$。

操作2："2 $x_1$ $y_1$ $x_2$ $y_2$"（不含双引号）。表示询问格子 $(x_1, y_1)$ 和格子 $(x_2,y_2)$ 之间的最短路的权值。$(1 \le x_1, x_2 \le 6, 1 \le y_1, y_2 \le n)$

对于每个操作 2，按照它在输入中出现的顺序，一次输出一行一个整数表示求得的最短路权值。

样例输入 1

5
0 0 1 0 0
0 1 0 1 0
0 2 0 1 0
0 1 1 1 0
0 0 0 0 0
1 1 1 1 1
5
2 1 2 1 4
1 1 1 10000
2 1 2 1 4
1 2 3 10000
2 1 2 3 3

样例输出 1

0
1
2

【数据约定】

测试数据规模如下表所示

屏幕快照 2019-06-18 下午2.59.58.png

【特别说明】

本题测试时将使用-O2优化。

（但comet 评测方法是统一的）

C0420 [WC2009-A]最短路问题

题目描述

输入格式

输出

样例

样例输入 1

样例输出 1

提示