Comet OJ

C0409 [NOI2018Day2-A]屠龙勇士

内存限制：512 MB 时间限制：2000 ms

题目描述

小 D 最近在网上发现了一款小游戏。游戏的规则如下：

  • 游戏的目标是按照编号1~n顺序杀掉n条巨龙，每条巨龙拥有一个初始的生命值$a_i$。同时每条巨龙拥有恢复能力，当其使用恢复能力时，它的生命值就会每次增加$p_i$，直至生命值非负。只有在攻击结束后且当生命值恰好为0时它才会死去。
  • 游戏开始时玩家拥有m把攻击力已知的剑，每次面对巨龙时，玩家只能选择一把剑，当杀死巨龙后这把剑就会消失，但作为奖励，玩家会获得全新的一把剑。

小 D 觉得这款游戏十分无聊，但最快通关的玩家可以获得 ION2018 的参赛资格， 于是小 D 决定写一个笨笨的机器人帮她通关这款游戏，她写的机器人遵循以下规则：

  • 每次面对巨龙时，机器人会选择当前拥有的，攻击力不高于巨龙初始生命值中攻击力最大的一把剑作为武器。如果没有这样的剑，则选择攻击力最低的一把剑作为武器。
  • 机器人面对每条巨龙，它都会使用上一步中选择的剑攻击巨龙固定的$x$次，使巨龙的生命值减少$x \times ATK$。
  • 之后，巨龙会不断使用恢复能力，每次恢复$p_i$生命值。若在使用恢复能力前或某一次恢复后其生命值为0，则巨龙死亡，玩家通过本关。

那么显然机器人的攻击次数是决定能否最快通关这款游戏的关键。小 D 现在得知了每条巨龙的所有属性，她想考考你，你知道应该将机器人的攻击次数$x$设置为多少，才能用最少的攻击次数通关游戏吗？

当然如果无论设置成多少都无法通关游戏，输出-1即可。

输入格式

第一行一个整数$T$，代表数据组数。

接下来$T$组数据，每组数据包含5行。

  • 每组数据的第一行包含两个整数，n和m，代表巨龙的数量和初始剑的数量；
  • 接下来一行包含n个正整数，第$i$个数表示第$i条巨龙的初始生命值$a_i$；
  • 接下来一行包含n个正整数，第$i$个数表示第$i$条巨龙的恢复能力$p_i$；
  • 接下来一行包含n个正整数，第$i$个数表示杀死第$i$条巨龙后奖励的剑的攻击力；
  • 接下来一行包含m个正整数，表示初始拥有的m把剑的攻击力。

输出

一共$T$行。

第$i$行一个整数，表示对于第$i$组数据，能够使得机器人通关游戏的最小攻击次数$x$，如果答案不存在，输出-1。

样例

样例输入 1

2
3 3
3 5 7
4 6 10
7 3 9
1 9 1000
3 2
3 5 6
4 8 7
1 1 1
1 1

样例输出 1

59
-1

提示

【样例 1 解释】

第一组数据：

  • 开始时拥有的剑的攻击力为{1,9,10}，第1条龙生命值为3，故选择攻击力为1的剑，攻击59次，造成59点伤害，此时龙的生命值为-56，恢复14次后生命值恰好为0，死亡。
  • 攻击力为1的剑消失，拾取一把攻击力为7的剑，此时拥有的剑的攻击力为{7,9,10}，第2条龙生命值为5，故选择攻击力为7的剑，攻击59次，造成413点伤害，此时龙的生命值为-408，恢复68次后生命值恰好为0，死亡。
  • 此时拥有的剑的攻击力为{3,9,10}，第3条龙生命值为7，故选择攻击力为3的剑，攻击59次，造成177点伤害，此时龙的生命值为-170，恢复17次后生命值恰好为0，死亡。
  • 没有比59次更少的通关方法，故答案为59。

第二组数据：

  • 不存在既能杀死第一条龙又能杀死第二条龙的方法，故无法通关，输出-1。

【子任务】

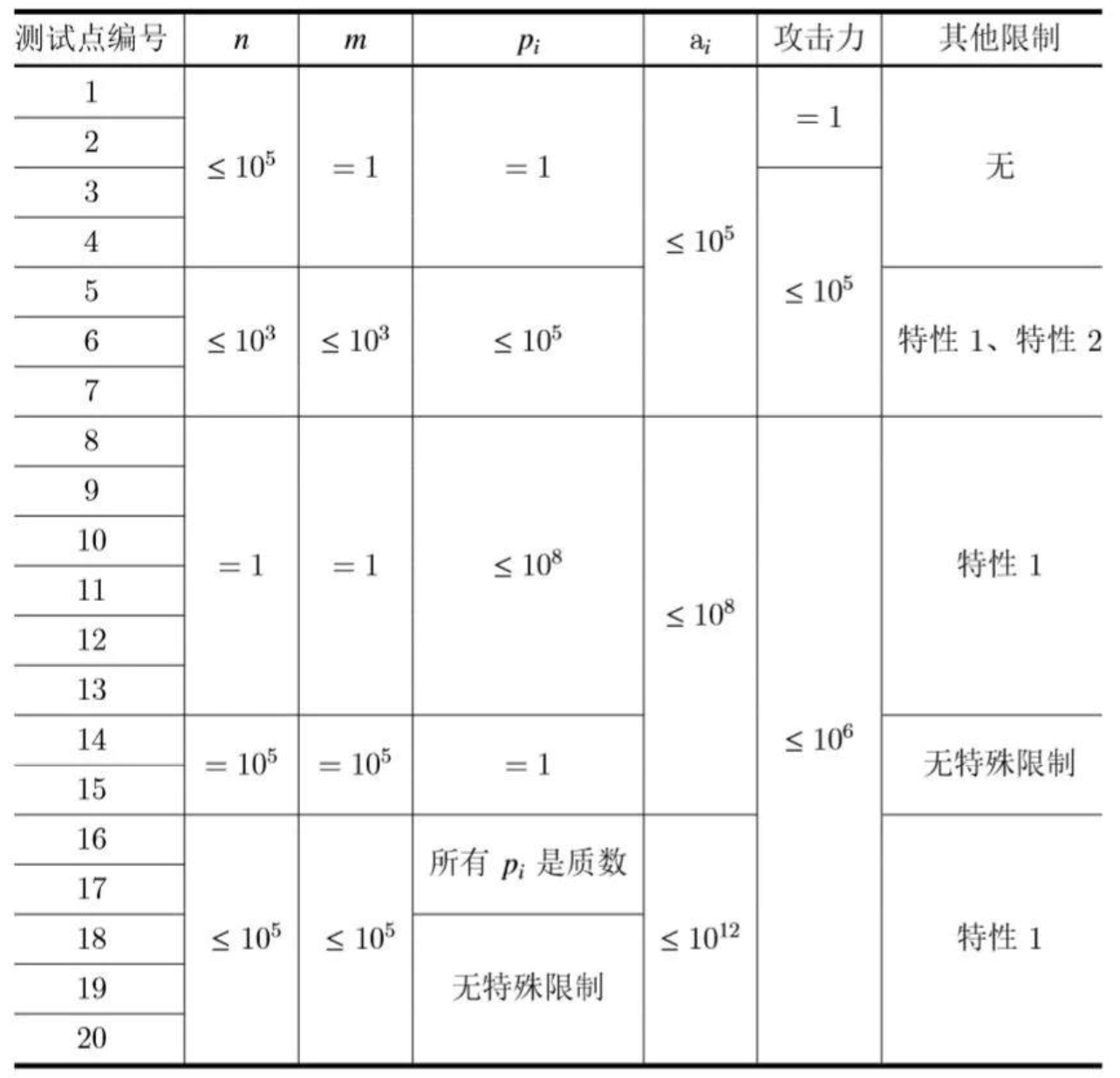
屏幕快照 2019-06-03 下午2.16.01.png

特性 1 是指：对于任意的$i$，$a_i \le p_i$。

特性 2 是指：$LCM(p_i) \le 10^6$，即所有的$p_i$最小公倍数不大于$10^6$。

对于所有的测试点，$T \le 5$，所有武器的攻击力$ \le 10^6$，所有$p_i$的最小公倍数$\le 10^{12}$。

【提示】

你所用到的中间结果可能很大，注意保存中间结果的变量类型。