C 国和 D 国近年来战火纷飞。
最近，C 国成功地渗透进入了 D 国的一个城市。这个城市可以抽象成一张有n个节点，节点之间由n-1条双向的边连接的无向图，使得任意两个点之间可以互相到达。也就是说，这张无向图实际上是一棵树。
经过侦查，C 国情报部部长 GGB 惊讶地发现，这座看起来不起眼的城市竟然是 D 国的军事中心。因此 GGB 决定在这个城市内设立情报机构。情报专家 TAC 在侦查后，安排了m种设立情报机构的方案。这些方案中，第$i$种方案是在节点$x_i$到节点$y_i$的最短路径的所有边上安排情报人员收集情报，这种方案需要花费$v_i$元的代价。
但是，由于人手不足，GGB 只能安排上述m种方案中的两种进行实施。同时 TAC 指出，为了让这两个情报机构可以更好的合作，它们收集情报的范围应至少有一条公共的边。为了评估一种方案的性能，GGB 和 TAC 对所有的边进行了勘察，给每一条边制定了一个情报价值$c_i$，表示收集这条边上的情报能够带来$c_i$元的收益。注意，情报是唯一的，因此当一条边的情报被两个情报机构收集时，也同样只会有$c_i$的收益。
现在，请你帮 GGB 选出两种合法的设立情报机构的方案进行实施，使得这两种方案收集情报的范围至少有一条公共的边，并且在此基础上总收益减去总代价的差最大。
注意，这个值可能是负的，但仍然是合法的。如果无法找到这样的两种方案，请输出F。
第一行包含一个整数$T$，表示数据组数；
每组数据包含（n+m+1）行：
第1行包含一个整数n，表示城市的点数；
第2到第n行中，第（i+1）行包含三个整数$a_i，b_i，c_i$，表示城市中一条连接节点$a_i$和$b_i$、情报价值为$c_i$的双向边，保证$a_i<b_i$且$b_i$互不相同；
第（n+1）行包含一个整数m，表示 TAC 设立的m种设立情报机构的方案；
第（n+2）到（n+m+1）行中，第（n+i+1）行包含三个整数$x_i，y_i，v_i$，表示第$i$种设立情报机构的方案是在节点$x_i$到节点$y_i$的最短路径上的所有边上安排情报人员收集情报，并且需要花费$v_i$元的代价。
包含$T$行；
对于每组数据，输出一行：如果存在合法的方案，则输出一个整数表示最大的总收益减去总代价的差；否则输出F。
Comet OJ2
5
1 2 1
2 3 3
3 4 2
1 5 8
2
1 4 5
3 5 8
5
1 2 1
2 3 3
3 4 3
1 5 9
2
1 5 5
2 3 81
F1
11
1 2 2
1 3 0
2 4 1
3 5 7
1 6 0
1 7 1
1 8 1
6 9 3
4 10 2
4 11 8
10
7 10 2
10 7 0
2 11 1
8 6 7
7 7 0
10 1 1
8 2 1
7 8 3
7 7 3
3 9 913【样例1解释】
这个样例中包含两组数据。这两组数据的城市相同，只是在情报的价值和情报机构的方案上有所不同。城市地图如下：
【样例2解释】
这一数据中，最优方案为选择第2种和第3种方案。
这组数据的城市地图如下，其中加粗的边表示被情报中心收集情报的边，红色的边表示只被第2种方案的情报中心收集情报的边，蓝色的边表示只被第3种方案的情报中心收集情报的边，紫色的边表示同时被两个情报中心收集情报的边。
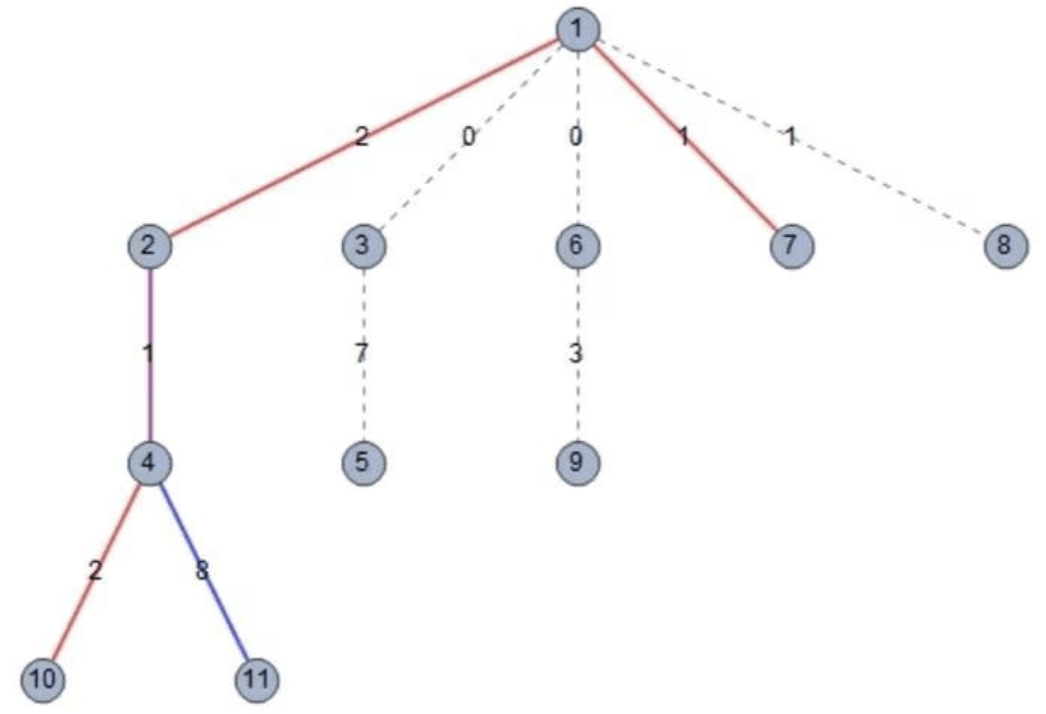
【子任务】
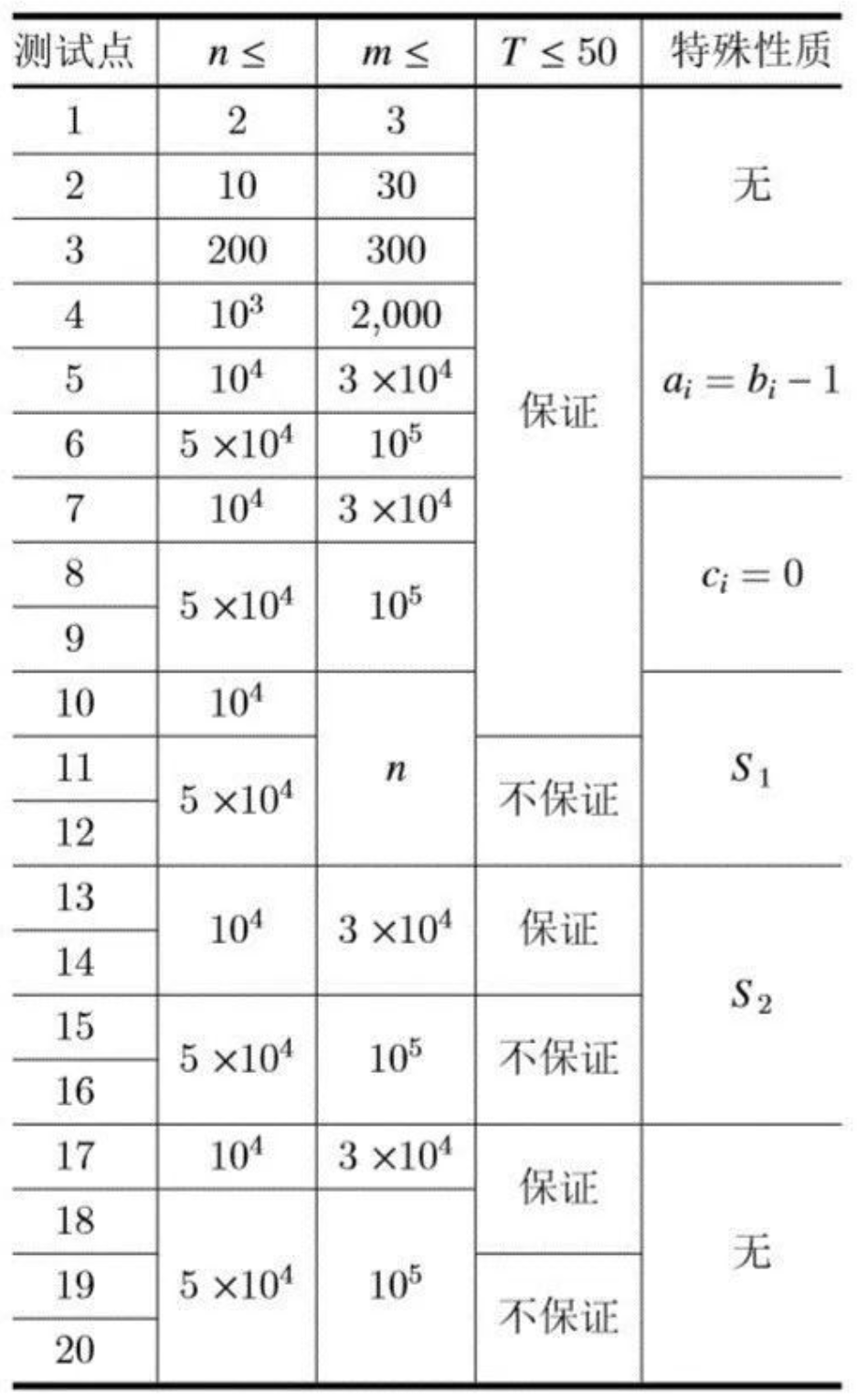
表格中的特殊性质如下：
特殊性质$S_1$：对于任意$i,j$，保证$x_i$到$y_i$的最短路径所经过的编号最小的节点不同于$x_j$到$y_j$的最短路径所经过的编号最小的节点；
特殊性质$S_2$：对于任意$i$，保证$x_i$到$y_i$的最短路径所经过的编号最小的节点为节点1。
对于所有的数据，$1\le n \le 5 \times 10^4，0 \le m \le 10^5，0 \le c_i \le 10^9，0 \le v_i \le 10^{10} \times n$。每个测试点中，所有n的和不会超过1000233，所有m的和不会超过2000233。