[NOI2017Day2-B]蔬菜

内存限制：512 MB 时间限制：3000 ms

小N是蔬菜仓库的管理员，负责设计蔬菜的销售方案。

在蔬菜仓库中，共存放有$n$种蔬菜，小N需要根据不同蔬菜的特性，综合考虑各方面因素，设计合理的销售方案，以获得最多的收益。

在计算销售蔬菜的收益时，每销售一个单位第$i$种蔬菜，就可以获得$a_i$的收益。

特别地，由于政策鼓励商家进行多样化销售，第一次销售第$i$种蔬菜时，还会额外得到$s_i$的额外收益。

在经营开始时，第$i$种蔬菜的库存为$c_i$个单位。

然而，蔬菜的保鲜时间非常有限，一旦变质就不能进行销售，不过聪明的小N已经计算出了每个单位蔬菜变质的时间：对于第$i$种蔬菜，存在保鲜值$x_i$，每天结束时会有$x_i$个单位的蔬菜变质，直到所有蔬菜都变质。（注意：每一单位蔬菜的变质时间是固定的，不随销售发生变化）

形式化地：对于所有的满足条件$d×x_i≤c_i$的正整数$d$，有$x_i$个单位的蔬菜将在第$d$天结束时变质。

特别地，若$(d−1)×x_i≤c_i<d×x_i$，则有$c_i−(d−1)×x_i$单位的蔬菜将在第$d$天结束时变质。

注意，当$x_i= 0$时，意味着这种蔬菜不会变质。

同时，每天销售的蔬菜总量也是有限的，最多不能超过$m$个单位。

现在，小N有$k$个问题，想请你帮忙算一算。每个问题的形式都是：对于已知的$p_j$，如果需要销售$p_j$天，最多能获得多少收益?

第一行包含三个正整数$n,m,k$，分别表示蔬菜的种类数目、每天能售出蔬菜总量上限、小N提出的问题的个数。

接下来$n$行，每行输入四个非负整数，描述一种蔬菜的特点，依次为$a_i,s_i,c_i,x_i$，意义如上文所述。

接下来$k$行，每行输入一个非负整数$p_j$，意义如上文所述。

输出$k$行，每行包含一个整数，第$i$行的数表示第$i$个问题的答案。

16
27

【样例1解释】

共有两种蔬菜：

销售第1种蔬菜时，每销售一单位可以获得的收益为3，第一次销售这种蔬菜时，额外可以获得的收益为3。这种蔬菜共有3个单位，均会在第一天结束时变质。

销售第2种蔬菜时，每销售一单位可以获得的收益为2，第一次销售这种蔬菜时，额外可以获得的收益为5。这种蔬菜共有8个单位，其中，有3单位在第一天结束时变质，3单位在第二天结束时变质，2单位在第三天结束时变质。

在只销售1天时，应当销售2单位的第一种蔬菜和1单位的第二种蔬菜。

在这种情况下：销售第一种蔬菜的收益为$2×3 + 3$；销售第二种蔬菜的收益为$1×2+5$；总共获得的收益为$(2×3+3)+(1×2+5) = 16$。

在只销售3天时，第一天应当销售3单位的第一种蔬菜，第二天应当销售3单位的第二种蔬菜（此时选择在第二天结束时会变质的3个单位出售），第三天销售2单位的第二种蔬菜。

在这种情况下：销售第一种蔬菜的收益为$3×3 + 3$；销售第二种蔬菜的收益为$(3+2)×2+5$；总共获得的收益为$(3×3+3)+[(3+2)×2+5] = 27$。

【子任务】

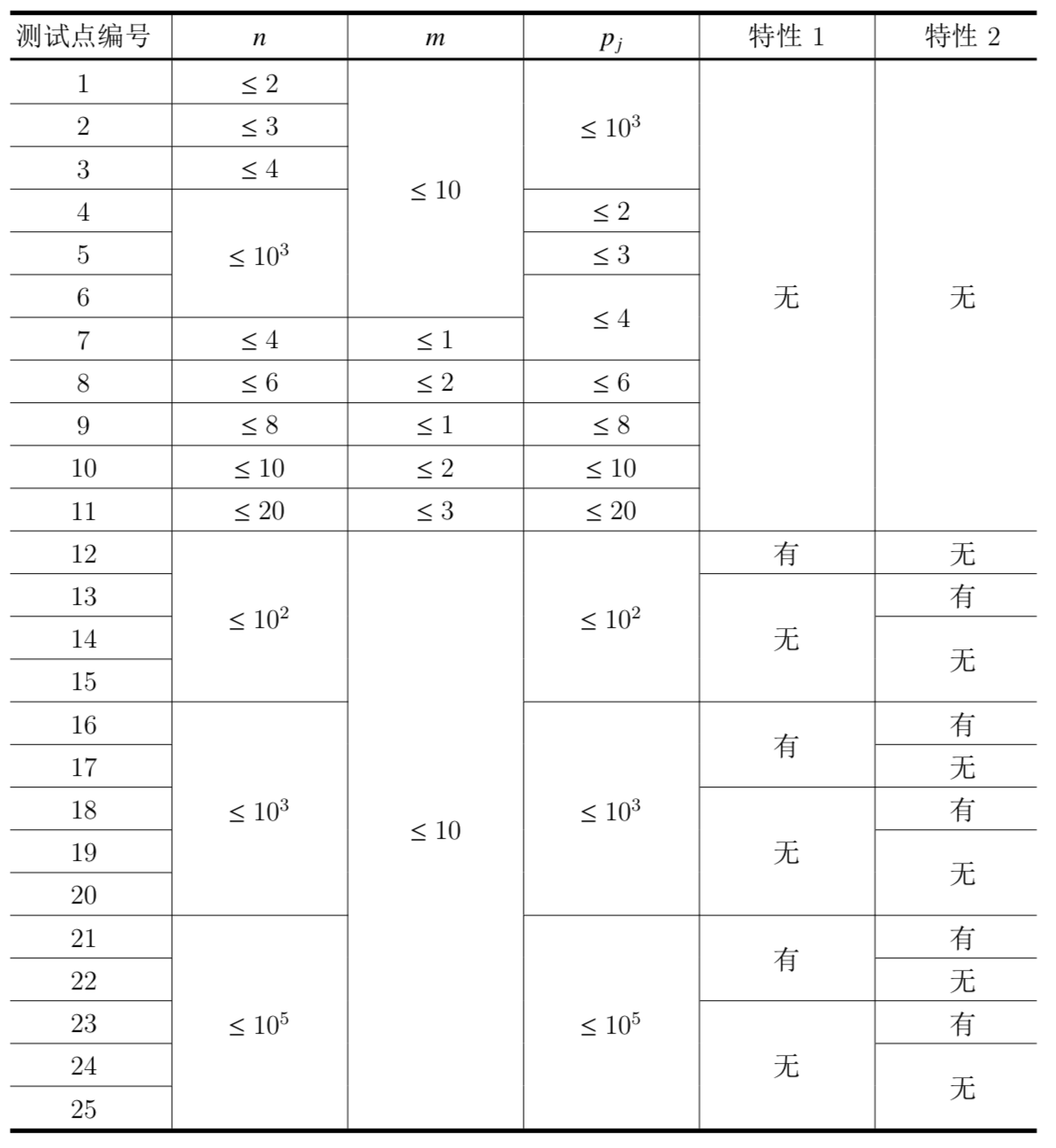
屏幕快照 2019-06-04 上午10.33.57.png

特性1：所有的$s_i$均为0。
特性2：所有的$x_i$均为0。
对于所有的测试数据，均保证$k$组询问中的$p_j$互不相同。
对于所有的测试数据，均保证$0<a_i,c_i≤10^9,0≤s_i,x_i≤10^9$。

C0403 [NOI2017Day2-B]蔬菜