C0402 [NOI2017Day2-C]分身术

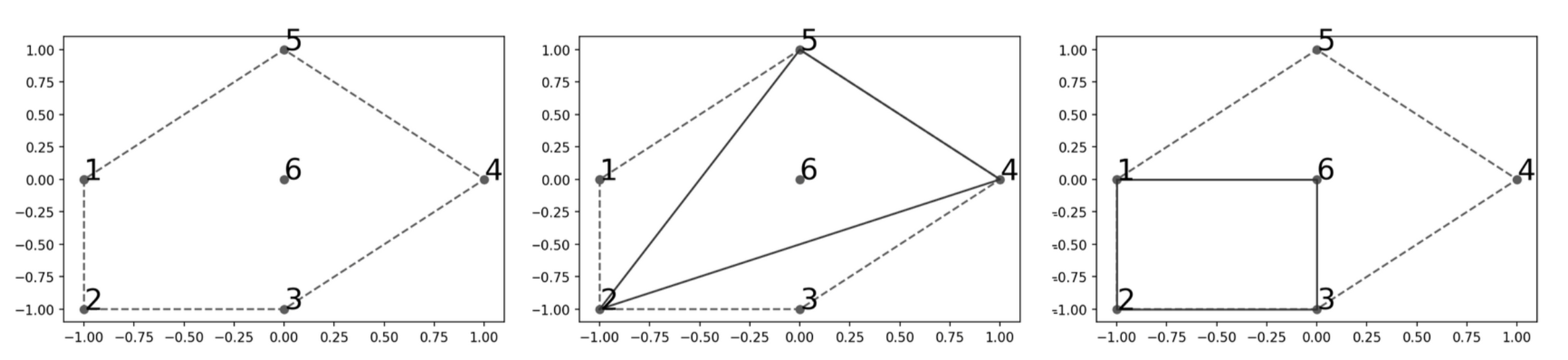
输入第一行包含两个正整数$n,m$，描述初始时分身的个数，和总时刻数。
接下来$n$行，第$i$行有两个整数$x_i,y_i$，描述第$i$个分身的位置。
接下来$m$行，每行的第一个整数$k$表示这一时刻有$k$个分身消失。接下来有$k$个非负整数$c_1,c_2,\cdots c_k$，用于生成消失的分身的编号。

生成方式如下：
设上一个时刻中，分身占领面积的两倍为S。则该时刻消失的分身$p_1,p_2, \cdots ,p_k$的编号为：$p_i= [(S+c_i)\bmod n] + 1$

特别的，在第一个时刻，我们认为上一个时刻中，$S=−1$，即：第一个时刻消失的分身$p_1,p_2,...,p_k$的编号为：$p_i= [(-1+c_i)\bmod n] + 1$

按给出时刻的顺序依次输出m行，每行一个整数，表示该时刻剩余分身所占领区域面积的两倍。

【样例1解释】

如下图所示：左图表示输入的6个分身的位置及它们占领的区域；中图表示第一个时刻的情形，消失的分身编号分别为1,3,6，剩余3个点占领图中实线内部区域，占据面积的两倍为3；右图表示第二个时刻的情形，消失的分身编号分别为
$[(0 + 3)\bmod6] + 1 = 4$
$[(1 + 3)\bmod6] + 1 = 5$

剩余的4个点占领图中实线内部区域。

【子任务】

对于所有数据，保证：

• $|x_i|,|y_i| ≤10^8$;

• 没有两个分身的坐标是完全相同的;

• $k≤100$;

• 所有时刻的$k$之和不超过$2×10^6$;

• $0≤c_i≤2_{31}−1$;

• 初始时，所有的$n$个分身占据区域面积大于0;

• 定义所有$n$个分身所占据区域的顶点集合为$S，|S| ≥3$。在任意时刻，S中至少存在两个未消失的分身。