C0401 [NOI2016Day1-A]优秀的拆分

第一行只有一个整数$𝑇$，表示数据的组数。保证$1≤𝑇≤10$。

接下来$𝑇$行，每行包含一个仅由英文小写字母构成的字符串$𝑆$，意义如题所述。

输出$𝑇$行，每行包含一个整数，表示字符串$𝑆$所有子串的所有拆分中，总共有多少个是优秀的拆分。

【样例1说明】

我们用$𝑆[𝑖,𝑗]$表示字符串$𝑆$第$𝑖$个字符到第$j$个字符的子串（从1开

始计数）。

第一组数据中，共有3个子串存在优秀的拆分：

𝑆[1,4] =aabb，优秀的拆分为𝐴 =a，𝐵 =b；
𝑆[3,6] =bbbb，优秀的拆分为𝐴 =b，𝐵 =b；
𝑆[1,6] =aabbbb，优秀的拆分为𝐴 =a，𝐵 =bb。

而剩下的子串不存在优秀的拆分，所以第一组数据的答案是3。

第二组数据中，有两类，总共4个子串存在优秀的拆分：

对于子串𝑆[1,4] = 𝑆[2,5] = 𝑆[3,6] =cccc，它们优秀的拆分相同，均为𝐴 =c，𝐵 =c，但由于这些子串位置不同，因此要计算3次；
对于子串𝑆[1,6] =cccccc，它优秀的拆分有2种：𝐴 =c，𝐵 =cc和𝐴 =cc，𝐵 =c，它们是相同子串的不同拆分，也都要计入答案。

所以第二组数据的答案是3 + 2 = 5。

第三组数据中，𝑆[1,8]和𝑆[4,11]各有2种优秀的拆分，其中𝑆[1,8]是问题描述中的例子，所以答案是2 + 2 = 4。

第四组数据中，𝑆[1,4]，𝑆[6,11]，𝑆[7,12]，𝑆[2,11]，𝑆[1,8]各有1种优秀的拆分，𝑆[3,14]有2种优秀的拆分，所以答案是5 + 2 = 7。

【子任务】

对于全部的测试点，保证$1 ≤ 𝑇 ≤ 10$。以下对数据的限制均是对于单组输入数据而言的，也就是说同一个测试点下的$𝑇$组数据均满足限制条件。

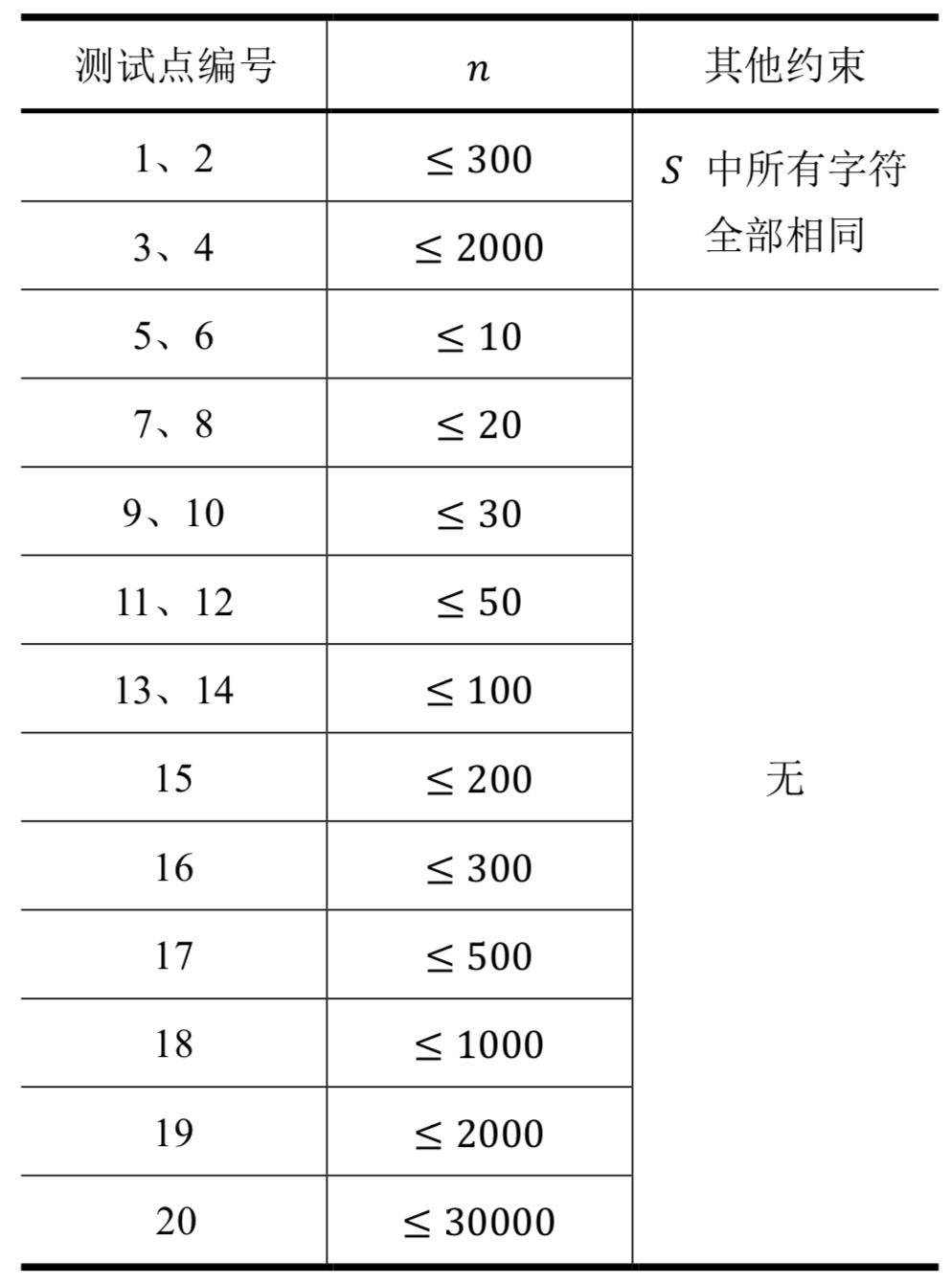
我们假定$𝑛$为字符串$𝑆$的长度，每个测试点的详细数据范围见下表：