[NOI2014Day1-A]起床困难综合症

内存限制：512 MB 时间限制：1000 ms

21世纪，许多人得了一种奇怪的病：起床困难综合症，其临床表现为：起床难，起床后精神不佳。作为一名青春阳光好少年，atm一直坚持与起床困难综合症作斗争。通过研究相关文献，他找到了该病的发病原因：在深邃的太平洋海底中，出现了一条名为drd的巨龙，它掌握着睡眠之精髓，能随意延长大家的睡眠时间。正是由于drd的活动，起床困难综合症愈演愈烈，以惊人的速度在世界上传播。为了彻底消灭这种病，atm决定前往海底，消灭这条恶龙。

历经千辛万苦，atm终于来到了drd所在的地方，准备与其展开艰苦卓绝的战斗。drd有着十分特殊的技能，他的防御战线能够使用一定的运算来改变他受到的伤害。具体说来，drd的防御战线由$𝑛$扇防御门组成。每扇防御门包括一个运算op和一个参数$𝑡$，其中运算一定是OR,XOR,AND中的一种，参数则一定为非负整数。如果还未通过防御门时攻击力为$𝑥$，则其通过这扇防御门后攻击力将变为$𝑥$ op $𝑡$。最终drd受到的伤害为对方初始攻击力$𝑥$依次经过所有$𝒏$扇防御门后转变得到的攻击力。

由于atm水平有限，他的初始攻击力只能为0到$𝑚$之间的一个整数（即他的初始攻击力只能在0, 1, ... , $𝑚$中任选，但在通过防御门之后的攻击力不受$𝑚$的限制）。为了节省体力，他希望通过选择合适的初始攻击力使得他的攻击能让drd受到最大的伤害，请你帮他计算一下，他的一次攻击最多能使drd受到多少伤害。

第1行包含2个整数，依次为$𝑛, 𝑚$，表示drd有$𝑛$扇防御门，atm的初始攻击力为0到$𝑚$之间的整数。

接下来$𝑛$行，依次表示每一扇防御门。每行包括一个字符串op和一个非负整数$𝑡$，两者由一个空格隔开，且op在前，$𝑡$在后，op表示该防御门所对应的操作，$𝑡$表示对应的参数。

输出一行一个整数，表示atm的一次攻击最多使drd受到多少伤害。

样例输入 1

3 10
AND 5
OR 6
XOR 7

样例输出 1

【样例说明】

atm可以选择的初始攻击力为0,1, ... ,10。

假设初始攻击力为4，最终攻击力经过了如下计算
4 AND 5 = 4
4 OR 6 = 6
6 XOR 7 = 1

类似的，我们可以计算出初始攻击力为1,3,5,7,9时最终攻击力为0，初始攻击力为0,2,4,6,8,10时最终攻击力为1，因此atm的一次攻击最多使drd受到的伤害值为1。

【数据规模与约定】

所有测试数据的范围和特点如下表所示

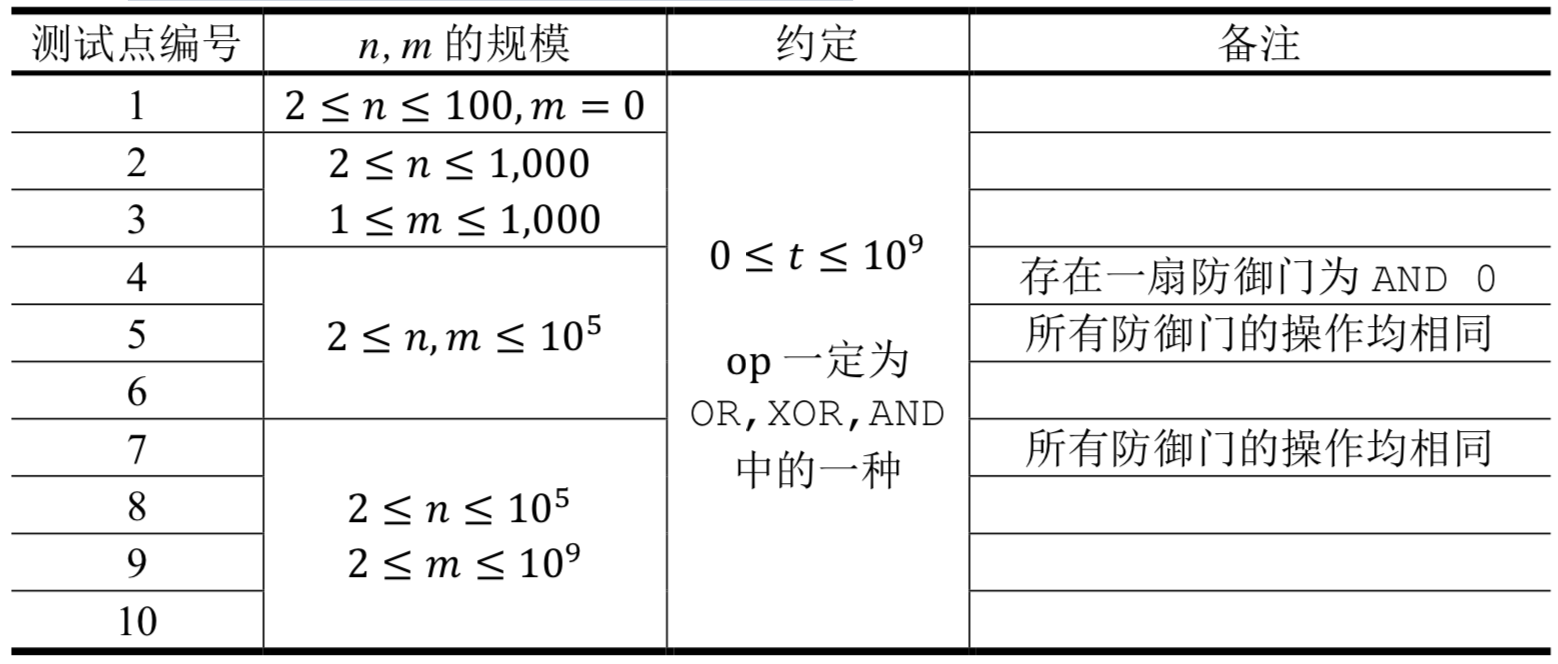
屏幕快照 2019-06-05 上午10.48.29.png

【运算解释】

在本题中，选手需要先将数字变换为二进制后再进行计算。如果操作的两个数二进制长度不同，则在前补0至相同长度。

OR为按位或运算，处理两个长度相同的二进制数，两个相应的二进制位中只要有一个为1，则该位的结果值为1，否则为0。XOR为按位异或运算，对等长二进制模式或二进制数的每一位执行逻辑异或操作。如果两个相应的二进制位不同（相异），则该位的结果值为1，否则该位为0。两个长度相同的二进制数，两个相应的二进制位都为否则为0。

例如，我们将十进制数5与十进制数3分别进行可以得到如下结果：

屏幕快照 2019-06-05 上午10.50.03.png

C0391 [NOI2014Day1-A]起床困难综合症

题目描述

输入格式

输出

样例

样例输入 1

样例输出 1

提示