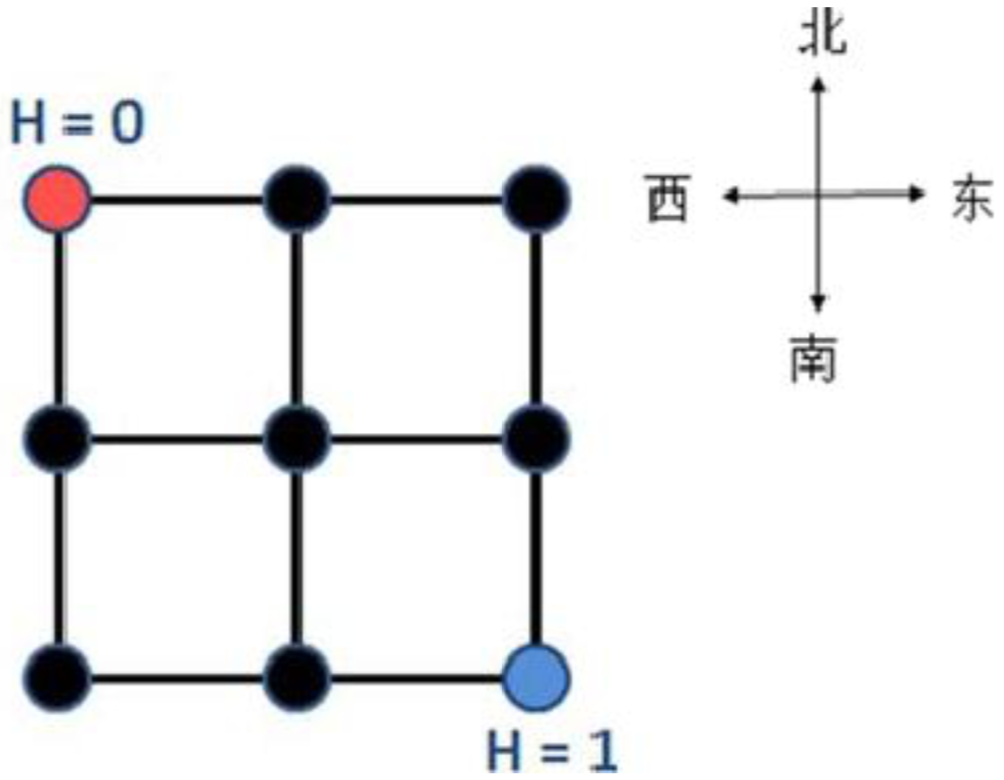
YT市是一个规划良好的城市,城市被东西向和南北向的主干道划分为$n×n$个区域。简单起见,可以将YT市看作 一个正方形,每一个区域也可看作一个正方形。从而,YT城市中包括$(n+1)×(n+1)$个交叉路口和$2n×(n+1)$条双向道路(简称道路),每条双向 道路连接主干道上两个相邻的交叉路口。下图为一张YT市的地图(n = 2),城市被划分为2×2个区域,包括3×3个交叉路口和12条双向道路。
小Z作为该市的市长,他根据统计信息得到了每天上班高峰期间YT市每条道路两个方向的人流量,即在高峰期间沿 着该方向通过这条道路的人数。每一个交叉路口都有不同的海拔高度值,YT市市民认为爬坡是一件非常累的事情,每向上爬h的高度,就需要消耗$h$的体力。如果 是下坡的话,则不需要耗费体力。因此如果一段道路的终点海拔减去起点海拔的值为$h$(注意h可能是负数),那么一个人经过这段路所消耗的体力是$max\{0, h\}$(这里$max\{a, b\}$表示取$a, b$两个值中的较大值)。
小Z还测量得到这个城市西北角的交叉路口海拔为0,东南角的交叉路口海拔为1(如上图所示),但其它交叉路口的海拔高度都无法得知。小Z想知道在最理想的情况下(即你可以任意假设其他路口的海拔高度),每天上班高峰期间所有人爬坡消耗的总体力和的最小值。