Black and white pictures are usually stored as bitmaps. A bitmap is a rectangular grid of pixels.
A polyline between pixels $P$ and $Q$ is a sequence of black pixels $P=P_1, P_2, …, P_k=Q$, where $P_i$ and $P_{i+1} ( i=1, …, k-1)$ are (vertically or horizontally) adjacent pixels. A polyline $P_1, P_2, ..., P_k$ is closed if $P_1=P_k$, and $P_i≠P_j (i=1, …, k-1, j=2, …, k)$ for $i<j$ unless $i=1$ and $j=k$ (that is the polyline does not contain the same pixel twice).
A set of black pixels $S$ is connected if for each pair of pixels $(P,Q)$ in $S$ there is at least one polyline $L$ between $P$ and $Q$ with all pixels of $L$ belonging to $S$.
A component of a bitmap is a maximal connected set of black pixels. A component may enclose holes. A hole consists of white pixels that are inside a closed polyline. A compact component encloses no holes.
Note that in Figure 1 the white pixel in the middle, marked with $x$, is not inside the highlighted closed polyline.
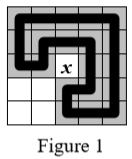
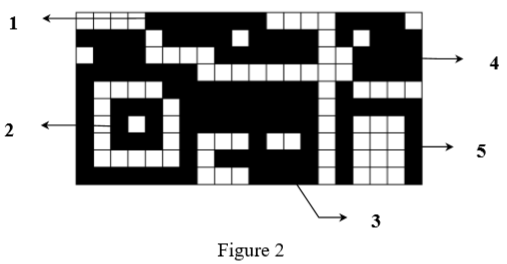
Figure 2 shows a bitmap with five components, of which two are compact ones.
You are to write a program that computes the total number of components and the number of compact components of a given coded bitmap.
Encoding. The bitmaps under investigation are coded (compressed) with the following method. Each row is coded with a sequence of integers $W_1, B_1, ..., W_k, B_k$, where $W_i$ is the number of consecutive white pixels, and Bi is the number of consecutive black pixels, respectively.
For example, the code of the first line of the bitmap in Figure 2 is the sequence 4 7 4 4 1 0. Components 4 and 5 are compact, while components 1, 2 and 3 are not compact.
The first line contains two positive integers, $N$ and $M$. $N (2 \le N \le 10000)$ is the number of rows and $M (2 \le M \le 1000)$ is the number of columns of the bitmap. The next $N$ lines contain the coded bitmap according to the paragraph on encoding. Each line terminates with -1.
The filemustcontain two lines, with a single integer in each line. The first line contains the number of all components and the second line contains the number of compact components of the input bitmap.
Comet OJ10 20
4 7 4 4 1 0 -1
0 4 1 4 1 4 1 1 1 3 -1
1 3 4 6 2 4 -1
0 7 9 4 -1
0 1 4 9 1 1 4 0 -1
0 1 1 3 1 8 1 5 -1
0 1 1 1 1 1 1 8 1 1 3 1 -1
0 1 1 3 1 1 3 1 2 1 1 1 3 1 -1
0 1 5 1 1 6 1 1 3 1 -1
0 7 3 4 1 1 3 1 -15
2GRADING
If the first line of your output file contains the correct number of all components, then you obtain 50% of the scores. If the second line of your output file contains the correct number of compact components, then you obtain an additional 50% of the scores.