C0238 [2018普及组-D]对称二叉树

第一行一个正整数$𝑛$，表示给定的树的节点的数目，规定节点编号1~n，其中节点1是树根。

第二行$𝑛$个正整数，用一个空格分隔，第$𝑖$个正整数$𝑣_𝑖$代表节点$𝑖$的权值。

接下来$𝑛$行，每行两个正整数$𝑙_i , 𝑟_i$，分别表示节点𝑖的左右孩子的编号。如果不存在左/右孩子，则以−1表示。两个数之间用一个空格隔开。

共一行，包含一个整数，表示给定的树的最大对称二叉子树的节点数。

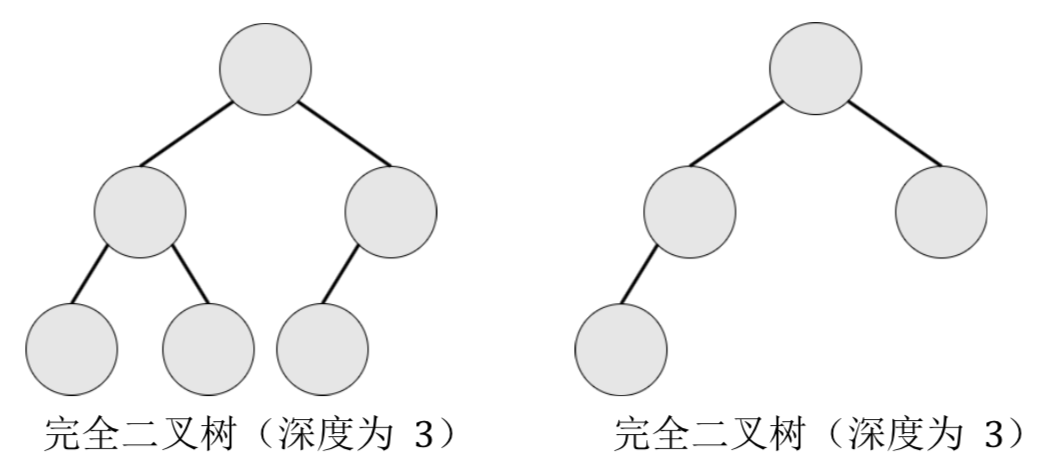
【输入输出样例1说明】

最大的对称二叉子树为以节点2为树根的子树，节点数为1。

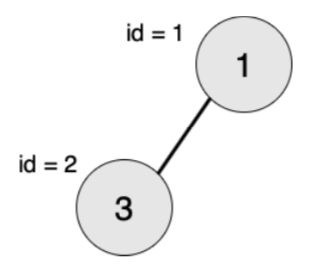
【输入输出样例2说明】

最大的对称二叉子树为以节点7为树根的子树，节点数为3。

【数据规模与约定】

共25个测试点。$𝑣_𝑖≤ 1000$。

测试点1~3，$𝑛 ≤ 10$，保证根结点的左子树的所有节点都没有右孩子，根结点的右子树的所有节点都没有左孩子。
测试点4~8，$𝑛 ≤ 10$。
测试点9~12，$𝑛 ≤ 10^5$，保证输入是一棵“满二叉树”。
测试点13~16，$𝑛 ≤ 10^5$，保证输入是一棵“完全二叉树”。
测试点17~20，$𝑛 ≤ 10^5$，保证输入的树的点权均为1。
测试点21~25，$𝑛 ≤ 10^6$。

本题约定：

层次：节点的层次从根开始定义起，根为第一层，根的孩子为第二层。树中任一节点的层次等于其父亲节点的层次加1。

树的深度：树中节点的最大层次称为树的深度。

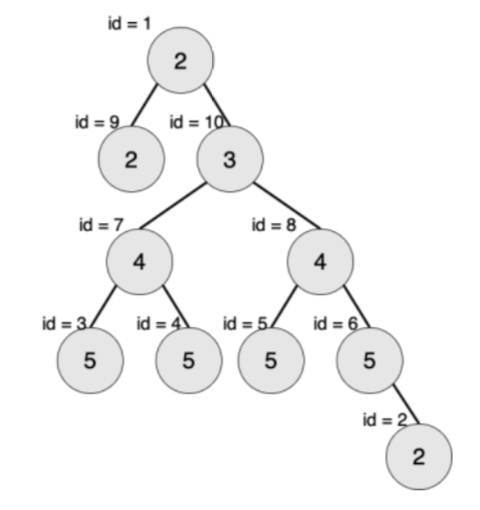
满二叉树：设二叉树的深度为h，且二叉树有$2^h− 1$个节点，这就是满二叉树。

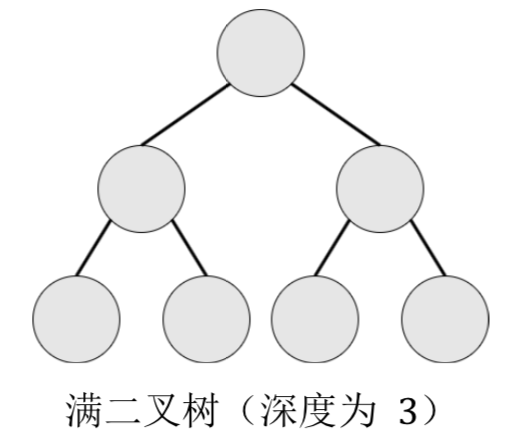
完全二叉树：设二叉树的深度为h，除第h层外，其它各层的结点数都达到最大个数，第h层所有的结点都连续集中在最左边，这就是完全二叉树。