【样例 1 说明】
对于第一个样例,装置屏幕将显示如下这些数对。
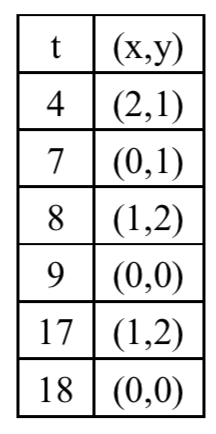
共有四个不同的数对:$(0,0),(0,1),(1,2),(2,1)$。
【数据范围与提示】
对于全部数据,$1 \le n \le 10^6,1 \le A,B \le 10^{18},0\le l_i \le r_i \le 10^{18},r_i < l_i+1$。
令 $S=\sum^n_{i=1}(r_i-l_i+1)$与$L=\max_{i=1}^n(r_i-l_i+1)$。
详细子任务附加限制与分值如下表。(comet 不支持APIO评分方式)
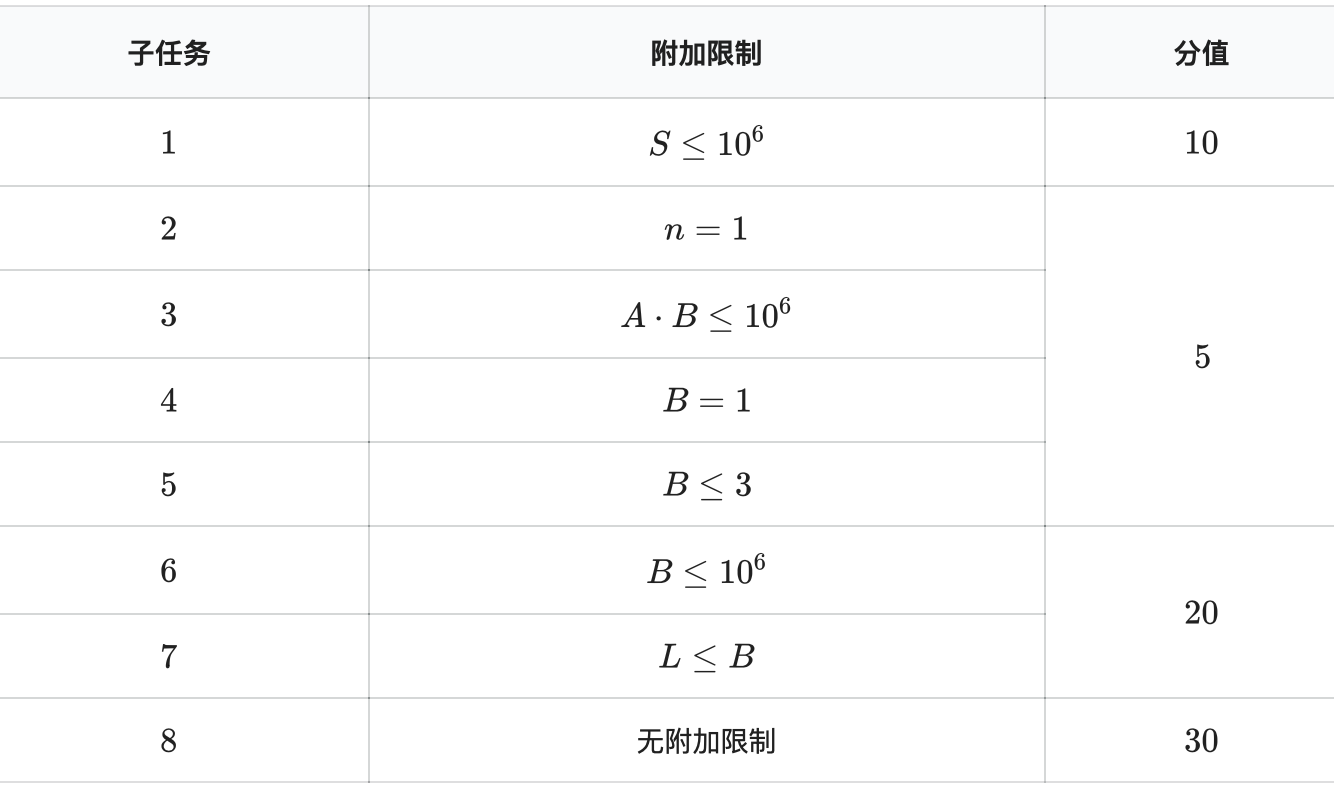
子任务 1:测试点 4-20
子任务 2:测试点 21-24
子任务 3:测试点 25-29
子任务 4:测试点 30-33
子任务 5:测试点 34-38
子任务 6:测试点 39-57
子任务 7:测试点 58-74
子任务 8:测试点 75-87