[2010普及组-C]导弹拦截

经过11年的韬光养晦，某国研发出了一种新的导弹拦截系统，凡是与它的距离不超过其工作半径的导弹都能够被它成功拦截。当工作半径为 $0$ 时，则能够拦截与它位置恰好相同的导弹。但该导弹拦截系统也存在这样的缺陷:每套系统每天只能设定一次工作半径。而当天的使用代价，就是所有系统工作半径的平方和。

某天，雷达捕捉到敌国的导弹来袭。由于该系统尚处于试验阶段，所以只有两套系统投入工作。如果现在的要求是拦截所有的导弹，请计算这一天的最小使用代价。

第一行包含 $4$ 个整数 $x_1、y_1、x_2、y_2$，每两个整数之间用一个空格隔开，表示这两套导弹拦截系统的坐标分别为($x_1, y_1$)、($x_2, y_2$)。

第二行包含 $1$ 个整数 $N$，表示有 $N$ 颗导弹。接下来 $N$ 行，每行两个整数 $x$、$y$，中间用一个空格隔开，表示一颗导弹的坐标 $(x, y)$。不同导弹的坐标可能相同。

输出只有一行，包含一个整数，即当天的最小使用代价。

【提示】
两个点 ($x_1, y_1$)、($x_2, y_2$) 之间距离的平方是 $(x_1−x_2)^2+(y_1−y_2)^2$。
两套系统工作半径 $r_1、r_2$ 的平方和，是指 $r_1、r_2$ 分别取平方后再求和，即 ${r_1}^2+{r_2}^2$。

【样例 $1$ 说明】
样例 $1$ 中要拦截所有导弹，在满足最小使用代价的前提下，两套系统工作半径的平方分别为 $18$ 和 $0$。

【样例 $2$ 说明】
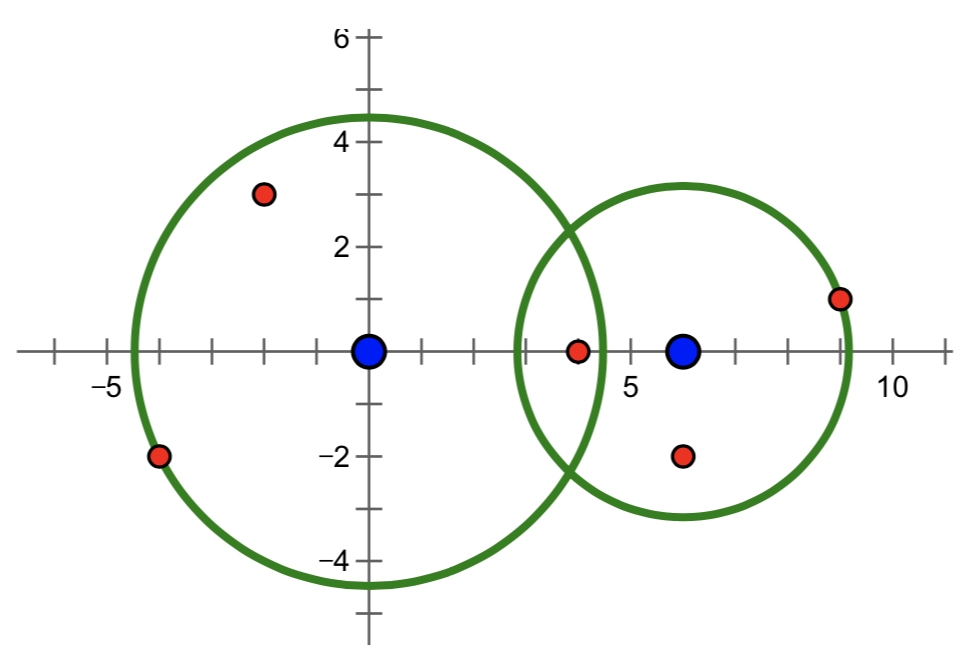
样例中的导弹拦截系统和导弹所在的位置如下图所示。要拦截所有导弹，在满足最小使用代价的前提下，两套系统工作半径的平方分别为 $20$ 和 $10$。

屏幕快照 2019-05-30 下午3.07.13.png

【数据范围】
对于 10% 的数据，$N = 1$
对于 20% 的数据，$1≤N≤2$
对于 40% 的数据，$1≤N≤100$
对于 70% 的数据，$1≤N≤1000$
对于 100% 的数据，$1≤N≤100000$，且所有坐标分量的绝对值都不超过 $1000$。

C0200 [2010普及组-C]导弹拦截