第一行为 $4$ 个整数 $L$ $R$ $m$ $n(0 \le L,R \le 10,1 \le m,n \le 50)$,其中 $L$ 代表强力炸弹的有效攻击距离,$R$ 代表神秘射线的作用半径,$m$ 和 $n$ 代表下水道平面图的规模。$x$ 坐标的范围为 $[1,m]$, $y$ 坐标的范围为 $[1,n]$。
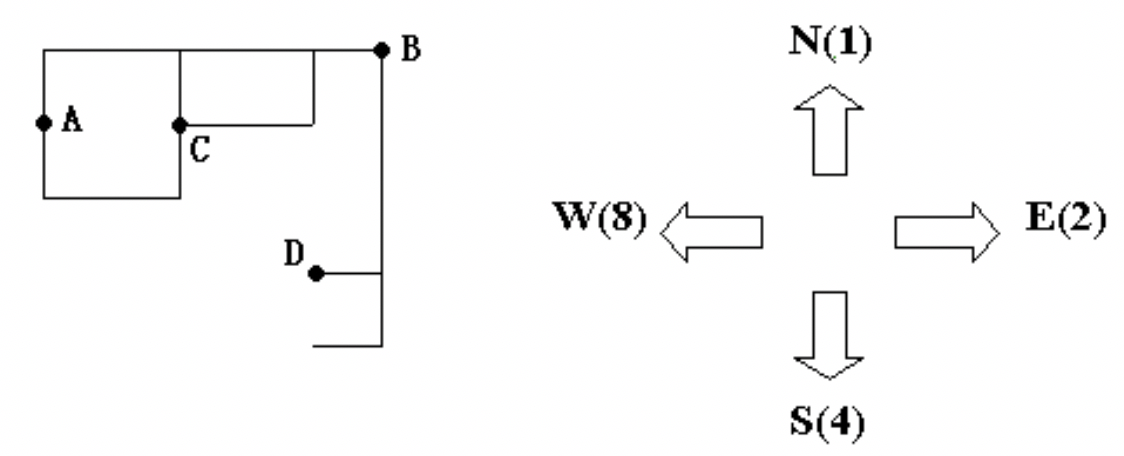
从第 $2$ 行到第 $m+1$ 行为下水道结构图。我们用方向数 $1$ 代表 N (北),用方向数 $2$ 代表 E (东),用方向数 $4$ 代表 S (南),用方向数 $8$ 代表 W (西)。第 $i+1$ 行的第 $j$ 个数字 $c_{i,j}$ 代表点 $(i,j)$ 处有管道连接的所有方向数之和,如上图中的点 B 的方向数之和为 $12$。
第 $m+2$ 行为一个整数 $K(1 \le K \le 50)$,代表时刻 $0$ 时老鼠的个数(此时老鼠都是成年的)。
第 $m+3$ 行到第 $m+K+2$ 行每行描述一只老鼠,包括该老鼠的初始坐标 $(x,y) (1 \le x \le m, 1 \le y \le n)$,朝向('E', 'S', 'W', 'N')以及性别('X'=雄,'Y'=雌)。输入保证每个老鼠都在水管内。
第 $m+K+3$ 行为两个整数 $P,Limit(1 \le P, Limit \le 100)$,分别表示特工队准备使用的武器个数以及控制鼠疫发生的老鼠数量的极限。
第 $m+K+4$ 行到第 $m+K+P+3$ 行每行描述一个武器,包括该武器的类型( 1 - 强力炸弹,2 - 神秘射线,3 - 定时炸弹,4 - 生物炸弹),放置的时刻 $t(t \ge 1)$,放置的坐标 $(x,y) (1 \le x \le m, 1 \le y \le n)$,输入保证武器放置在管道内。武器按照放置的时间不降序排列。
最后一行包含一个整数 $Time(1 \le Time \le 1000)$,表示模拟的结束时刻。$Time$ 保证比所有武器的放置时刻大。