Comet OJ

C0147 [2018提高组Day1-C]赛道修建

内存限制：512 MB 时间限制：1000 ms

题目描述

C 城将要举办一系列的赛车比赛。在比赛前，需要在城内修建 $𝑚$ 条赛道。

C 城一共有 $𝑛$ 个路口，这些路口编号为 $1,2, ... , 𝑛$，有 $𝑛 − 1$ 条适合于修建赛道的双向通行的道路，每条道路连接着两个路口。其中，第 $𝑖$ 条道路连接的两个路口编号为 $𝑎_𝑖$ 和 $𝑏_𝑖$，该道路的长度为 $𝑙_𝑖$。借助这 $𝑛−1$ 条道路，从任何一个路口出发都能到达其他所有的路口。

一条赛道是一组互不相同的道路 $𝑒_1, 𝑒_2, ... , 𝑒_𝑘$，满足可以从某个路口出发，依次经过道路 $𝑒_1, 𝑒_2, ... , 𝑒_𝑘$（每条道路经过一次，不允许调头）到达另一个路口。一条赛道的长度等于经过的各道路的长度之和。为保证安全，要求每条道路至多被一条赛道经过。

目前赛道修建的方案尚未确定。你的任务是设计一种赛道修建的方案，使得修建的 $𝑚$ 条赛道中长度最小的赛道长度最大（即 $𝑚$ 条赛道中最短赛道的长度尽可能大）。

输入格式

输入第一行包含两个由空格分隔的正整数 $𝑛, 𝑚$，分别表示路口数及需要修建的赛道数。

接下来 $𝑛 − 1$ 行，第 $𝑖$ 行包含三个正整数 $𝑎_𝑖, 𝑏_𝑖, 𝑙_𝑖$，表示第 $𝑖$ 条适合于修建赛道的道路连接的两个路口编号及道路长度。保证任意两个路口均可通过这 $𝑛 − 1$ 条道路相互到达。每行中相邻两数之间均由一个空格分隔。

输出

输出共一行，包含一个整数，表示长度最小的赛道长度的最大值。

样例

样例输入 1

7 1
1 2 10
1 3 5
2 4 9
2 5 8
3 6 6
3 7 7

样例输出 1

31

样例输入 2

9 3
1 2 6
2 3 3  
3 4 5
4 5 10
6 2 4
7 2 9
8 4 7
9 4 4

样例输出 2

15

提示

【样例 1 说明】

所有路口及适合于修建赛道的道路如下图所示：

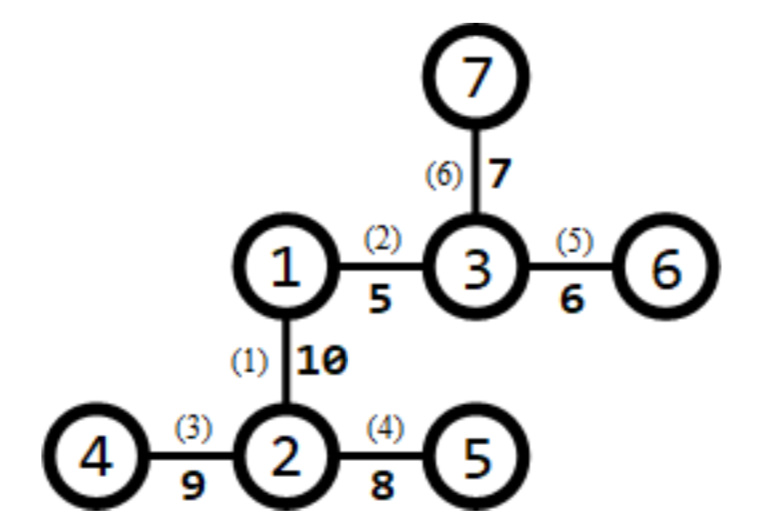
屏幕快照 2019-05-21 下午3.11.00.png

道路旁括号内的数字表示道路的编号，非括号内的数字表示道路长度。

需要修建 $1$ 条赛道。可以修建经过第 $3,1,2,6$ 条道路的赛道从（路口 $4$ 到路口 $7$），则该赛道的长度为 $9 + 10 + 5 + 7 = 31$，为所有方案中的最大值。

【样例 2 说明】

所有路口及适合于修建赛道的道路如下图所示：

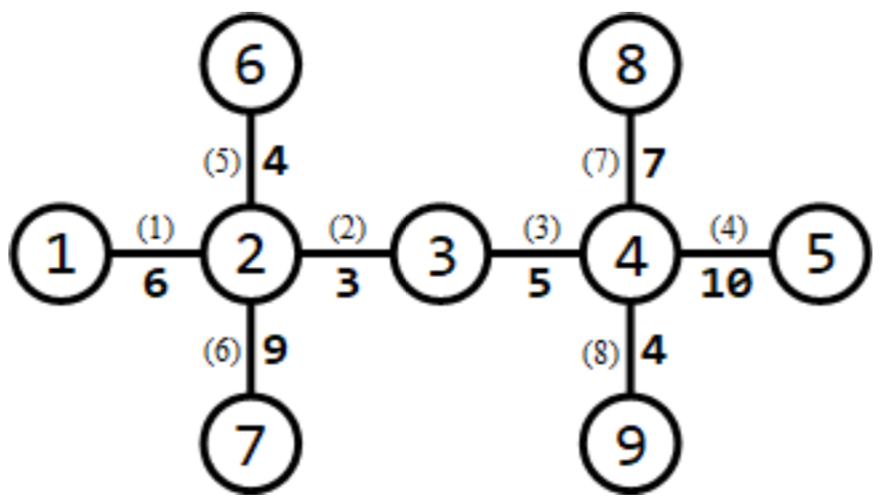
屏幕快照 2019-05-21 下午3.14.19.png

需要修建 $3$ 条赛道。可以修建如下 $3$ 条赛道：

  1. 经过第 $1,6$ 条道路的赛道（从路口 $1$到路口 $7$），长度为 $6 + 9 = 15$;
  2. 经过第 $5,2,3,8$ 条道路的赛道（从路口 $6$ 到路口 $9$），长度为 $4 + 3 + 5 + 4 = 16$;
  3. 经过第 $7,4$ 条道路的赛道（从路口 $8$ 到路口 $5$），长度为 $7 + 10 = 17$。

长度最小的赛道长度为 $15$，为所有方案中的最大值。


【数据规模与约定】

所有测试数据的范围和特点如下表所示

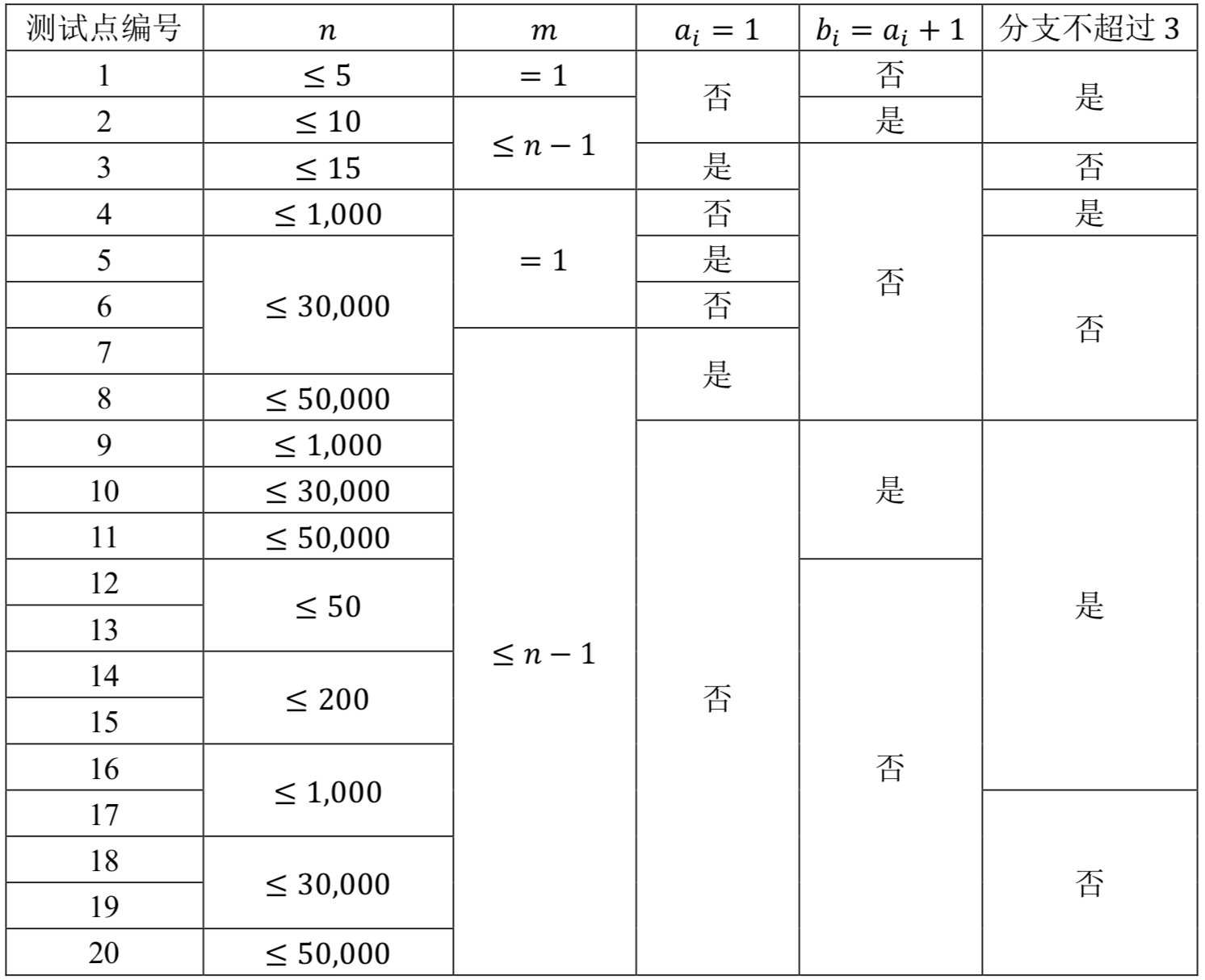
屏幕快照 2019-05-21 下午3.19.45.png

其中，“分支不超过 3”的含义为：每个路口至多有 $3$ 条道路与其相连。对于所有的数据，$2≤𝑛≤50,000，1≤𝑚≤𝑛−1，1≤𝑎_𝑖,𝑏_𝑖≤𝑛，1≤𝑙_𝑖≤10,000$。