Comet OJ

C0110 [CTSC2017]最长上升子序列

内存限制：512 MB 时间限制：1000 ms

题目描述

猪小侠最近学习了最长上升子序列的相关知识。对于一个整数序列 $A =(a_1, a_2, \cdots , a_k)$，定义 $A$ 的子序列为：从 $A$ 中删除若干个元素后（允许不删，也允许将所有 $k$ 个元素都删除），剩下的元素按照原来的顺序所组成的序列。如果这个子序列的元素从左到右严格递增，则称它为 $A$ 的一个上升子序列。其中包含元素数量最多的上升子序列称为 $A$ 的最长上升子序列。例如， $(2, 4, 5, 6)$ 和 $(1, 4, 5, 6)$ 都是 $(2, 1, 1, 4, 7, 5, 6)$ 的最长上升子序列，长度都为 $4$。

现在猪小侠遇到了这样一个问题：给定一个序列 $B_m = (b_1, b_2, \cdots , b_m)$，设 $C$ 是 $B_m$ 的子序列，且 $C$ 的最长上升子序列的长度不超过 $k$，则 $C$ 的长度最大能是多少？

猪小侠觉得这个问题太简单了，缺乏挑战，他决定提出一个更难的问题。于是他给了你这样一个序列 $B = (b_1, b_2, \cdots , b_n)$，以及若干次询问。每次询问会给定两个整数 $m$ 和 $k$，你需要对于 $B$ 序列的前 $m$ 个元素构成的序列 $B_m = (b_1, b_2, \cdots , b_m)$ 和 $k$ 回答上述问题。

输入格式

第一行两个整数 $n, q$，其中 $n$ 是序列 $B$ 的长度， $q$ 是询问次数。

第二行是空格隔开的 $n$ 个正整数 $b_1, b_2, \cdots , b_n$。

接下来 $q$ 行，其中第 $i$ 行包含两个整数 $m_i, k_i$，表示对 $m = m_i, k = k_i$ 进行询问。

输出

输出共 $q$ 行，按顺序每行一个整数作为回答。

样例

样例输入 1

11 6
9 6 3 1 5 12 8 4 2 2 2
5 1
7 2
9 1
9 2
11 1
11 11

样例输出 1

4 
6 
5 
8 
7
11

样例输入 2

1

样例输出 2

1

提示

【样例1解释】

询问 1：对于序列 (9,6,3,1,5)，可以选取子序列 (9,6,3,1)，它的最长上升子序列长度为 1。

询问 2：对于序列 (9,6,3,1,5,12,8)，可以选取子序列 (9,6,3,1,12,8)，它的最长上升子序列长度为 2。

询问 3：对于序列 (9,6,3,1,5,12,8,4,2)，可以选取子序列 (9,6,5,4,2)，它的最长上升子序列长度为 1。

询问 4：对于序列 (9,6,3,1,5,12,8,4,2)，可以选取子序列 (9,6,3,1,12,8,4,2)，它的最长上升子序列长度为 2。

询问 5：对于序列 (9,6,3,1,5,12,8,4,2,2,2)，可以选取子序列 (9,6,5,4,2,2,2)，它的最长上升子序列长度为 1。

询问 6：对于序列 (9,6,3,1,5,12,8,4,2,2,2)，可以选取子序列 (9,6,3,1,5,12,8,4,2,2,2)，它的最长上升子序列长度为 3。

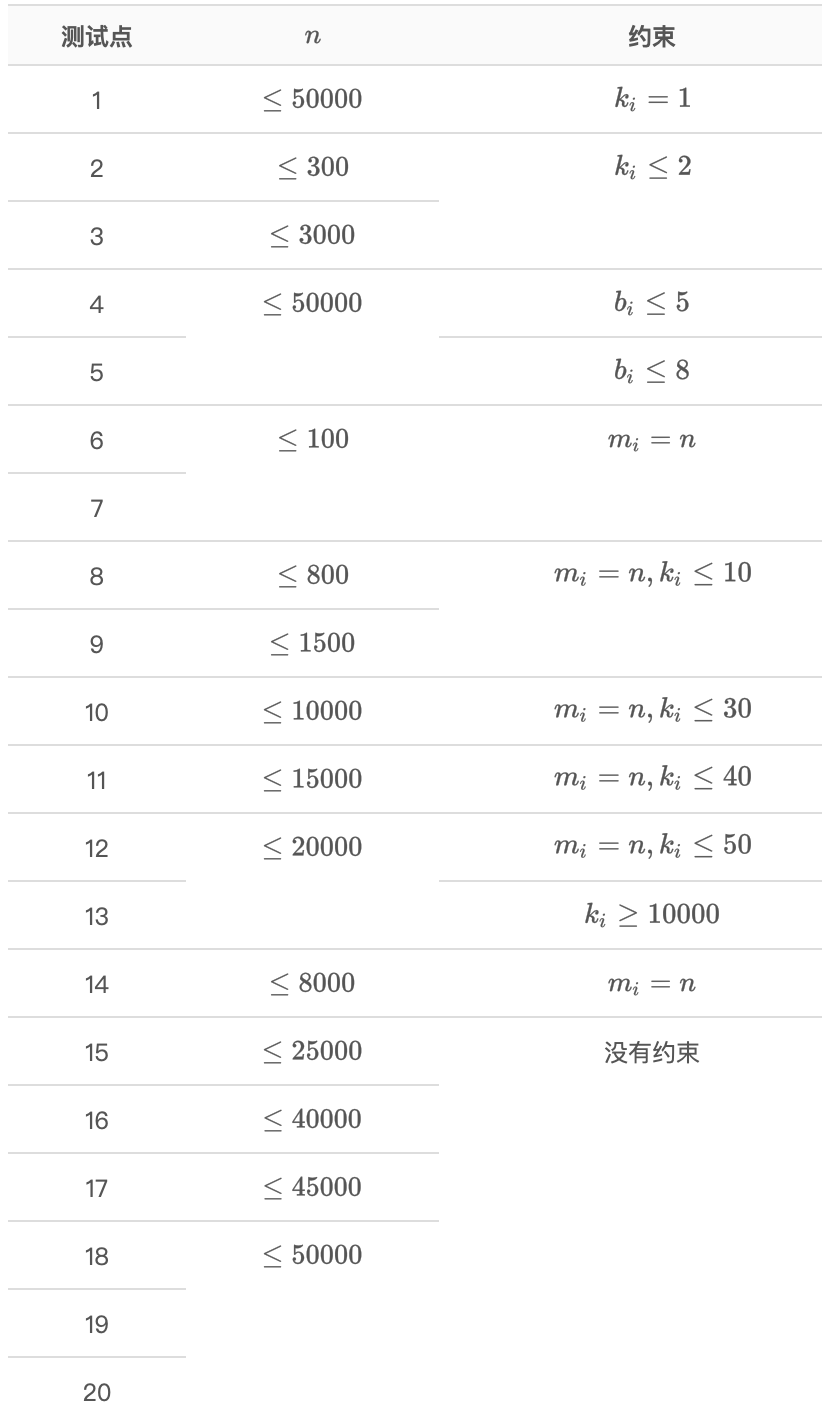
【数据范围与约定】

屏幕快照 2019-07-08 下午6.46.47.png