Comet OJ

C0058 [2006提高组-B]金明的预算方案

内存限制：256 MB 时间限制：1000 ms

题目描述

金明今天很开心，家里购置的新房就要领钥匙了，新房里有一间金明自己专用的很宽敞的房间。更让他高兴的是，妈妈昨天对他说：“你的房间需要购买哪些物品，怎么布置，你说了算，只要不超过 $N$ 元钱就行”。今天一早，金明就开始做预算了，他把想买的物品分为两类：主件与附件，附件是从属于某个主件的，下表就是一些主件与附件的例子：

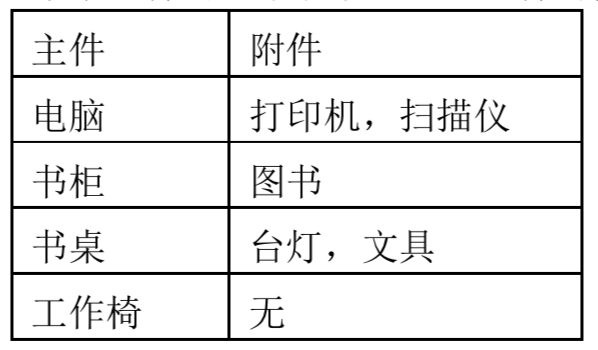
屏幕快照 2019-05-27 下午12.43.33.png

如果要买归类为附件的物品，必须先买该附件所属的主件。每个主件可以有 $0$ 个、$1$ 个或 $2$ 个附件。附件不再有从属于自己的附件。金明想买的东西很多，肯定会超过妈妈限定的 $N$ 元。于是，他把每件物品规定了一个重要度，分为 $5$ 等：用整数 $1$~ $5$ 表示，第 $5$ 等最重要。他还从因特网上查到了每件物品的价格（都是 $10$ 元的整数倍）。他希望在不超过 $N$ 元（可以等于 $N$ 元）的前提下，使每件物品的价格与重要度的乘积的总和最大。

设第 $j$ 件物品的价格为 $v[j]$，重要度为 $w[j]$，共选中了 $k$ 件物品，编号依次为 $j_1，j_2，…，j_k$，则所求的总和为：

$v[j_1] \times w[j-1]+v[j_2] \times w[j_2]+…+v[j_k] \times w[j_k]$。

请你帮助金明设计一个满足要求的购物单。

输入格式

第 $1$ 行为两个正整数 $N, m$，用一个空格隔开。其中 $N$（$<32000$）表示总钱数，$m$（$<60$）为希望购买物品的个数。

从第 $2$ 行到第 $m+1$ 行，第 $j$ 行给出了编号为 $j-1$ 的物品的基本数据，每行有 $3$ 个非负整数 $v,p,q$。其中 $v$ 表示该物品的价格（$v<10000$）， $p$ 表示该物品的重要度（$1$~ $5$），$q$ 表示该物品是主件还是附件。如果 $q=0$，表示该物品为主件，如果 $q>0$，表示该物品为附件，$q$ 是所属主件的编号。

输出

只有一个正整数，为不超过总钱数的物品的价格与重要度乘积的总和的最大值 $(<200000)$。

样例

样例输入 1

1000 5
800 2 0
400 5 1
300 5 1
400 3 0
500 2 0

样例输出 1

2200

提示